Оценка безопасности движения транспортных средств на прямолинейном участке дороги

Аннотация: В статье рассматривается безопасность движения транспортных средств на прямолинейном участке дороги. Оценивается возможность возникновения дорожно-транспортного происшествия при внезапном торможении впереди идущего автомобиля по какой-либо причине. Для обеспечения безопасности движения и предотвращения снижения пропускной способности дороги из-за возникновения дорожно-транспортного происшествия транспортные средства, движущиеся по прямолинейному участку дороги большой протяженности должны соблюдать расстояние, определенное по формулам.

Ключевые слова: пропускная способность дороги, дорожно-транспортное происшествие, безопасность движения, минимально-безопасное расстояние.

дорожный торможение расстояние безопасность Транспортные средства, как правило, развивают наибольшую скорость на прямолинейном участке дороги большой протяженности [5−7]. При этом увеличивается опасность возникновения дорожно-транспортного происшествия и, как следствие, уменьшение пропускной способности дороги на какой-то промежуток времени [8−10].

Оценим возможность возникновения дорожно-транспортного происшествия при внезапном торможении впереди идущего автомобиля по какой-либо причине.

Рассмотрим следующую дорожную ситуацию при движении автомобилей и в попутном направлении: автомобиль, имеющий скорость, догоняет впереди движущийся со скоростью автомобиль, т. е. выполняется неравенство.

. (1).

Постановка задачи. На каком минимально-безопасном расстоянии должен находиться автомобиль от автомобиля, чтобы в случае применения экстренного торможения водителем автомобиля водитель автомобиля мог предотвратить столкновение.

Результат решения поставленной задачи приводится в [1, 3], однако при каких условиях им можно пользоваться не указано.

За начальный момент времени принимаем момент обнаружения водителем автомобиля момента начала торможения водителем автомобиля. Считаем, что автомобили и в начальный момент времени имели скорости и соответственно, причем скорости удовлетворяют неравенству (1).

При выполнении неравенств.

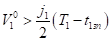
(2).

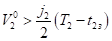
. (3).

Законы изменения скорости движения и длины пути пройденного автомобилями и определены в [2]. Время движения автомобиля до полной остановки определяется равенством.

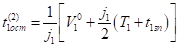
. (4).

Время движения автомобиля до полной остановки определяется равенством.

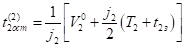
. (5).

Отметим, что в рассматриваемом случае оба автомобиля оставят на дороге тормозной след всех своих колес, если тормозная система автомобилей исправна.

С) Пусть выполняются неравенства.

. (6).

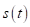
Выражения функций и определены в [4].

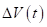
Рассмотрим несколько случаев.

С 1) Пусть выполняется неравенство .

На полуинтервале функция имеет вид.

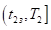
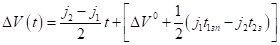
Моментом времени, подозрительным на безопасный момент касания, на полуинтервале будет точка, определенная равенством.

.

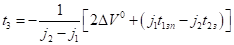
Теперь рассмотрим разность.

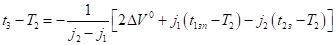
. (7).

С 1.1) Пусть выполняется неравенство.

. (8).

Тогда разность (7) меньше нуля, следовательно, выполняется неравенство.

(9).

Из неравенства (9) следует, что. Так как коэффициент при в выражении функции на полуинтервале положительный в силу, то функция принимает на сегменте отрицательные значения, а на полуинтервале положительные значения. Следовательно, при выполняется неравенство.

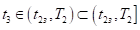
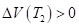
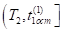
. (10).

Рассмотрим полуинтервал. Функция на этом полуинтервале имеет вид.

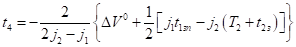
(11).

а момент времени подозрительный на безопасный момент касания определяется равенством.

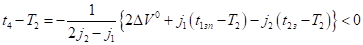
. (12).

Отметим, выполнение неравенства.

. (13).

Проверим, принадлежит ли момент времени полуинтервалу. Для этого рассмотрим сначала разность.

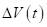
в силу неравенств (8) и (13). Следовательно, выполняется неравенство.

. (14).

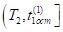
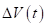
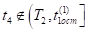
Отсюда следует, что. Так как коэффициент при в выражении функции на полуинтервале положительный в силу неравенства (13) и выполняется неравенство (14), то функция принимает на полуинтервале положительные значения. Следовательно, при выполняется неравенство.

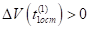
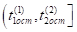
. (15).

С 1.1.1) Пусть в неравенствах (6) выполняется строгое неравенство.

. (16).

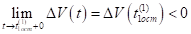
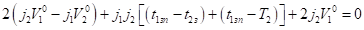
Очевидно, что функция на полуинтервале принимает отрицательные значения. Но тогда, что противоречит неравенству (15). Полученное противоречие показывает, что при выполнении неравенств (6), (16) неравенство (8) выполняться не может.

С 1.1.2) Пусть в условиях (6) выполняется равенство.

. (17).

Равенство (17) может быть записано в виде.

.

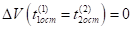
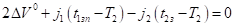
Но тогда будет выполняться равенство, которое противоречит неравенству (15). Полученное противоречие показывает, что при выполнении неравенств (6) и равенства (17) неравенство (8) выполняться не может.

С 1.2) Пусть выполняется равенство.

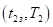
. (18).

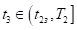
Тогда разность (7) равна нулю, следовательно, выполняется равенство, что означает. Так как коэффициент при в выражении функции на полуинтервале положительный в силу, то функция принимает на сегменте отрицательные значения. При выполняется равенство.

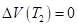
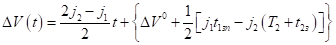
. (19).

Рассмотрим полуинтервал. Функция на этом полуинтервале имеет вид (11),.

.

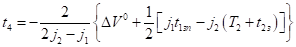
а момент времени подозрительный на безопасный момент касания определяется равенством (12).

.

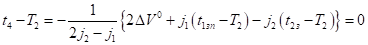
Из равенства (18) следует, что разность.

.

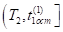
следовательно.

. (20).

Так как коэффициент при в выражении функции на полуинтервале положительный в силу, то функция принимает на этом полуинтервале положительные значения. При выполняется неравенство (15).

.

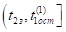
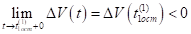
Таким образом, получили, что при переходе через точку функция меняет знак с «» на ««, следовательно, момент времени является безопасным моментом касания на полуинтервале .

С 1.2.1) Пусть в неравенствах (6) выполняется строгое неравенство (16).

.

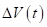
Очевидно, что функция на полуинтервале принимает отрицательные значения. Но тогда, что противоречит неравенству (15). Полученное противоречие показывает, что при выполнении неравенств (6), (16) равенство (18) выполняться не может.

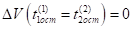
С 1.1.2) Пусть в условиях (6) выполняется равенство (17).

.

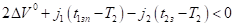
Но тогда будет выполняться равенство, которое противоречит неравенству (15). Полученное противоречие показывает, что при выполнении неравенства (6) и равенства (17) равенство (18) выполняться не может.

С 1.3) Пусть выполняется неравенство.

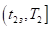
. (21).

Тогда разность (7) больше нуля, следовательно, выполняется неравенство.

. (22).

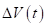
Так как коэффициент при в выражении функции на полуинтервале положительный и выполняется неравенство (22), то функция принимает на этом полуинтервале отрицательные значения. При выполняются неравенства.

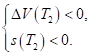
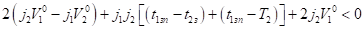
Функция на полуинтервале имеет вид (11), а момент времени подозрительный на безопасный момент касания определяется равенством (12).

С 1.3.1) Пусть в неравенствах (6) выполняется строгое неравенство (16).

.

Неравенство (16) может быть записано в виде.

. (23).

Рассмотрим разность.

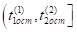
. (24).

Разность (24) положительна в силу неравенств (13) и (23). Отсюда следует, что выполняется неравенство.

(25).

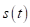
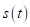
Очевидно, что функция на полуинтервале принимает отрицательные значения. Получили, что при выполнении неравенств (6), (16), (21) функция достигает отрицательного наименьшего значения при .

С 1.1.2) Пусть в условиях (6) выполняется равенство (17).

.

Тогда разность (23) равна нулю, следовательно, выполняются равенства.

.

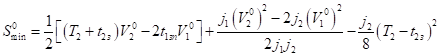
Тогда получаем, что при выполнении неравенств (6), (21) и равенства (17) функция достигает отрицательного наименьшего значения при .

Минимально-безопасное расстояние в этом случае определяется равенством.

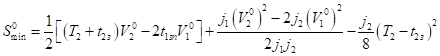
. (26).

Для обеспечения безопасности движения и предотвращения снижения пропускной способности дороги из-за возникновения дорожно-транспортного происшествия транспортные средства, движущиеся по прямолинейному участку дороги большой протяженности должны соблюдать расстояние, определенное по формулам 26.

Например, расстояние между автомобилями, исключающее возможность возникновения дорожно-транспортного происшествия, движущимися со скоростями V₁ = 15 м/с и V₂ = 20 м/с, определенное по формуле 26 составляет 28,98 м.

• 1. Иларионов В. А. Экспертиза дорожно-транспортных происшествий. М.: Транспорт, 1989. 255 c.
• 2. Карев Б. Н., Сидоров Б. А., Недоростов П. М. Методы расчета безопасных расстояний при попутном движении транспортных средств: монография. Екатеринбург: Урал. гос. лесотехн. ун-т., 2005. 315 с.
• 3. Суворов Ю. Б. Судебная дорожно-транспортная экспертиза. М.: Экзамен, 2003. 208 c.
• 4. Филатова Н. А., Габдорахманов А. С., Карев Б. Н. Нахождение минимально-безопасного расстояния между автомобилями, движущимися в попутном направлении, в одном частном случае // Научное творчество молодежи — лесному комплексу России: матер. XII всерос. науч.-техн. конф. — Екатеринбург: Урал. гос. лесотехн. ун-т, 2016, ч.1. 365 с.
• 5. Бояркина Е. Ф., Логачев В. Г. Имитационное моделирование процесса формирования количества легковых автомобилей на улично-дорожной сети города // Инженерный вестник Дона, 2015, № 3. URL: ivdon.ru/ru/magazine/archive/n3y2015/3254.
• 6. Быков Д. В., Лихачёв Д. В. Имитационное моделирование как средство модернизации участка транспортной сети // Инженерный вестник Дона, 2014, № 2. URL: ivdon.ru/ru/magazine/archive/n2y2014/2388.
• 7. Феофилова А. А. Обоснование выбора состояний транспортных потоков для начала их динамического перераспределения // Инженерный вестник Дона, 2013, № 3. URL: ivdon.ru/ru/magazine/archive/n3y2013/1953.
• 8. Гасилова О. С., Алексеева О. В., Грехов О. Ю. Влияние интенсивности движения маршрутных транспортных средств на пропускную способность улично-дорожной сети // Инженерный вестник Дона, 2016, № 4. URL: ivdon.ru/ru/magazine/archive/n4y2016/3808.
• 9. Highway Capacity Manual 2000. Transportation Research Board, National Research Council. Washington, D.C., USA, 2000. 1134 p.
• 10. Zyryanov V., Sanamov R. Improving urban public transport operation: experience of Rostov-on-Don (Russia) // International Journal of Transport Economics. 2009. V.36. № 1. pp.83−96.

References.

• 1. Ilarionov V.A. Jekspertiza dorozhno-transportnyh proisshestvij [Examination of road accidents]. M.: Transport, 1989. 255 p.
• 2. Karev B.N., Sidorov B.A., Nedorostov P.M. Metody rascheta bezopasnyh rasstojanij pri poputnom dvizhenii transportnyh sredstv [ Methods of calculation of safe distances at the passing movement of vehicles]: monografija. Ekaterinburg: Ural. gos. lesotehn. un-t., 2005. 315 p.
• 3. Suvorov Ju.B. Sudebnaja dorozhno-transportnaja jekspertiza [Judicial road and transport examination]. M.: Jekzamen, 2003. 208 p.
• 4. Filatova N.A., Gabdorahmanov A.S., Karev B.N. Nauchnoe tvorchestvo molodezhi — lesnomu kompleksu Rossii: mater. XII vseros. nauch.-tehn. konf. Ekaterinburg: Ural. gos. lesotehn. un-t, 2016, ch.1. 365 p.
• 5. Bojarkina E.F., Logachev V.G. Inћenernyj vestnik Dona (Rus), 2015, № 3. URL: ivdon.ru/ru/magazine/archive/n3y2015/3254.
• 6. Bykov D.V., Lihachjov D.V. Inћenernyj vestnik Dona (Rus), 2014, № 2. URL: ivdon.ru/ru/magazine/archive/n2y2014/2388.
• 7. Feofilova A.A. Inћenernyj vestnik Dona (Rus), 2013, № 3. URL: ivdon.ru/ru/magazine/archive/n3y2013/1953.
• 8. Gasilova O.S., Alekseeva O.V., Grehov O.Ju. Inћenernyj vestnik Dona (Rus), 2016, № 4. URL: ivdon.ru/ru/magazine/archive/n4y2016/3808.
• 9. Highway Capacity Manual 2000. Transportation Research Board, National Research Council. Washington, D.C., USA, 2000. 1134 p.
• 10. Zyryanov V., Sanamov R. International Journal of Transport Economics. 2009. V.36. № 1. pp.83−96.