Разделение общего уравнения на два

Уравнение (7.3) можно свести к системе двух волновых уравнений, если представить вектор перемещений следующим образом: u = gradtp + rot у, т.с. если разложить вектор перемещений на эквиволюмиальную (волны искажений) и безвихревую составляющие. Здесь <�р и у/ — скалярный и векторный потенциалы.

Подставим и в уравнение (7.3):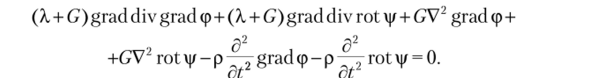

Поскольку¹ divgrad (p = V²

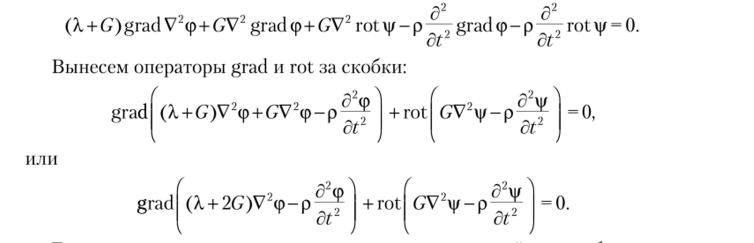
Если дивергенция и ротор поля определены в каждой точке ооласти, то всюду в этой области функция может быть представлена в виде суммы безвихревого ноля и соленоидального поля (теорема разложения Гельмгольца)². На основании этой теоремы имеем.

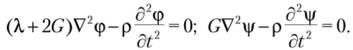
В итоге получим два волновых уравнения.

Плоские волны

Если в некоторой точке упругой среды возникнет какое-либо возмущение, то из этой точки во все стороны начнут распространяться волны. На большом расстоянии от центра возмущения эти волны можно рассматривать как плоские и считать, что все частицы смещаются параллельно на-^[1]

правлению движения волны (продольные волны) или перпендикулярно этому направлению (поперечные волны). В первом случае это будут волны расширения-сжатия, во втором — сдвига.

Если для продольной волны выбрать направление распространения волны вдоль оси х, то v = w = 0, а и будет функцией только х. В этом случае первое уравнение (7.6) примет вид.

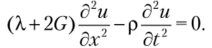
Запишем его как волновое уравнение:

Путем подстановки доказывается, что решением уравнения (7.10) являются любые функции и, = /,(х + с,?) и и., =/₂(х — с/). Следовательно, общее решение можно представить в форме.

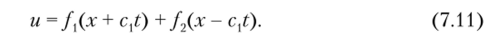
Это решение имеет простую физическую интерпретацию. Рассмотрим второй член в правой части формулы (7.11). Для любого заданного времени t этот член является функцией только одной переменной х и может быть представлен некоторой кривой линией (рис. 7.1), форма которой зависит от вида функции /₂. Через интервал времени At аргумент функции /₂ примет вид х — с,(? + At). Значение функции /₂ останется неизменным, если одновременно с увеличением t на величину At абсцисса увеличится на величину Дх, равную с, Л/. Это означает, что кривая, построенная для момента времени t, может также использоваться для момента t + At, если ее сместить в направлении х на расстояние Дх = с, Д?, как показано на рис. 7.1 штриховой линией. Также можно доказать, что первый член решения (7.11) представляет волну, движущуюся в противоположном направлении. Таким образом, общее решение (7.11) представляет две волны, движущиеся вдоль оси х в противоположных направлениях с постоянной скоростью с, определяемой формулой (7.8). Эту формулу можно записать через модуль упругости и коэффициент 11уассона:

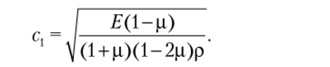
Например, для стали можно принять с, = 6070 м/с.

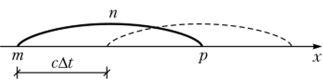
Рис. 7.1. Движение плоской волны Рассмотрим теперь поперечные волны. Если ось х направлена в сторону распространения волны, а ось у имеет поперечное направление, то перемещения и и wбудут равны нулю, а перемещение v будет функцией х и I. Тогда из уравнений (7.4) имеем Это уравнение имеет тот же вид, что и уравнение (7.10). Поэтому можно сделать тот же вывод, что волны сдвига распространяются вдоль оси х со скоростью с₂. Как и для уравнения (7.10), любая функция f{x — c₂t) является решением уравнения (7.12). Ниже приводится таблица приближенных значений скоростей распространения волн в грунте (табл. 7.1)^[2]

Таблица 7.1

Приближенные значения скоростей распространения волн в грунте.

• [1] Корн Г., Корн Т. Справочник по математике. М.: Наука, 1974. 2 См. там же.
• [2] Филиппов И. Г., Егорычев О. А. Нестационарные колебания и дифракция волн в акустических и упругих средах. М.: Машиностроение, 1977.