Аналитическая геометрия. 
Основы высшей математики

Аналитическая геометрия, раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р. Декарту, изложившему ее основы в последней главе своего трактата Рассуждение о методе, озаглавленной Геометрия (1637). Однако сам метод был известен П. Ферма еще в 1629, о чем свидетельствует его переписка. Аналитическая геометрия стала неоценимым подспорьем для математического анализа, изобретенного вскоре Ньютоном (1665−1666) и Лейбницем (1675−1676).

Методы аналитической геометрии применимы к фигурам на плоскости и к поверхностям в трехмерном пространстве, а также допускают естественное обобщение и на пространства более высоких размерностей. Мы начнем с аналитической геометрии на плоскости.

Сущность метода координат состоит в следующем. На плоскости задаются две взаимно перпендикулярные прямые (координатные оси), пересекающиеся в точке О, называемой началом координат. Одна из них — ось x, или ось абсцисс, обычно выбирается горизонтальной, другая — ось y, или ось ординат, — вертикальной. Справа от O выбирается точка, у которой ставится отметка 1. Если принять отрезок от O до 1 за единицу длины, то откладывая последовательно этот отрезок вдоль прямой, мы получаем числовую ось. Считается, что эта ось продолжается вправо до бесконечности. Точки на оси x слева от O помечаются отрицательными числами, как на шкале термометра. Например, точка ?2 расположена от точки O слева на таком же расстоянии, как точка 2 справа. Аналогичным образом с той же единицей длины размечается и ось y. Положительные числа располагаются выше точки O, отрицательные — ниже.

Пусть P — любая точка на плоскости с заданной системой координат, Q — основание перпендикуляра, опущенного из P на ось x, а R — основание перпендикуляра, опущенного из P на ось y. Положение точки P полностью определяется двумя числами, называемыми координатами x и y. Первая координата указывает положение точки Q на оси x, вторая — положение точки R на оси y. На рис. 1 положение точки P полностью определяется ее координатами (2,3).

Основная задача аналитической геометрии заключается в изучении геометрических фигур с помощью соотношений между координатами точек, из которых эти фигуры образованы. Любую фигуру можно рассматривать как множество точек, удовлетворяющих некоторому геометрическому условию. Это условие можно записать в виде алгебраического уравнения, связывающего координаты x и y каждой точки фигуры. Суть метода аналитической геометрии состоит в изучении свойств фигуры с помощью соответствующего уравнения, исследуемого средствами алгебры. Этот метод позволяет устанавливать геометрические факты систематичным образом, в отличие от традиционной «синтетической» геометрии, где приходилось изобретать методы доказательства для каждого отдельного случая.

Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками P₁ = (x₁, y₁) и P₂ = (x₂, y₂). Числа x₁, y₁, x₂ и y₂ могут быть любыми действительными числами, положительными, отрицательными или 0. На рис. 2 все числа выбраны положительными. Проведем через точку P₁ горизонтальную прямую, а через точку P₂ — вертикальную. Пусть R — точка их пересечения. Тогда по теореме Пифагора.

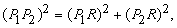
Откуда.

d ² = (x₂ — x₁)² + (y₂ — y₁)².

Это и есть формула для вычисления расстояния между двумя точками.

Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки P₁ и P₂. Например, если точка P₂ расположена ниже точки P₁ и справа от нее, как на рис. 3, то отрезок RP₂ можно считать равным y₁ — y₂, а не y₂ — y₁. Расстояние между точками, вычисляемое по формуле, от этого не изменится, так как (y₁ — y₂)² = (y₂ — y₁)². Заметим, что так как величина y₂ в этом случае отрицательна, разность y₁ — y₂ больше, чем y₁, как и должно быть.

Прямая — одна из простейших геометрических фигур. Алгебраическое уравнение прямой также имеет простой вид.

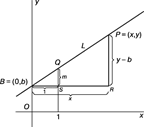
Пусть B = (0,b) — точка пересечения прямой L с осью y, а P = (x, y) — любая другая точка на этой прямой. Проведем через точку B прямую, параллельную оси x, а через точку P — прямую, параллельную оси y; проведем также прямую x = 1. Пусть m — угловой коэффициент прямой L (см. рис. 4). Так как треугольники BSQ и BRP подобны, то.

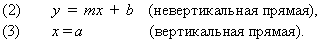
или, после упрощения, Следовательно, если точка P лежит на прямой L, то ее координаты удовлетворяют уравнению (1). Обратно, нетрудно показать, что если x и yсвязаны между собой уравнением (1), то точка P непременно лежит на прямой L, проходящей через точку (0,b) и имеющей угловой коэффициентm.

Таким образом, уравнение любой прямой можно записать в виде.

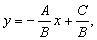
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени по x и y можно привести к виду (2) либо (3).

Рассмотрим произвольное уравнение первой степени Если B № 0, мы можем записать уравнение (4) в виде.

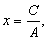
т.е. в виде (2). При B = 0 уравнение (4) сводится к уравнению.

Ax = C,.

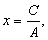
т.е. к уравнению вида (3).

Таким образом, любая прямая описывается уравнением первой степени поx и y, и обратно, каждое уравнение первой степени по x и y соответствует некоторой прямой.