Изображение синусоидальных функций в комплексной форме

Для анализа и расчета электрических цепей синусоидального тока применяют комплексный метод, базирующийся на теории комплексных чисел.

Любой вектор А на плоскости, проведенный из начала координат и изображающий действующее значение ЭДС, напряжения или тока однозначно определяется точкой, соответствующей концу этого вектора (точка А на рис. 2.6). При этом модуль вектора равен действующему значению (А), а угол между вектором и осью вещественных чисел Яе равен начальной фазе (у/). На плоскости комплексных чисел точке А соответствует одно комплексное число А. Таким образом, любой вектор, проведенный из начала координат, однозначно изображается комплексным числом, соответствующим координатам конца этого вектора. Комплексный метод расчета применим только к цепям с синусоидальными ЭДС, напряжениями и токами, так как только синусоидальные величины можно изображать векторами.

Вектор А имеет вещественную (а) и мнимую (Ь) составляющие:

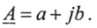
Координаты точки А могут быть выражены через длину вектора |ОЛ| = А и угол у/: а = Асозу/, Ь = Аь’ту/. Тогда вектор в комплексном виде.

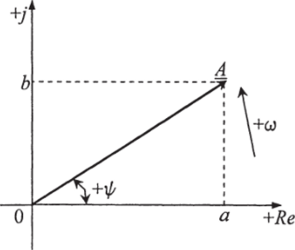
Рис. 2.6. Составляющие ком плексного числа на ком' плексной плоскости.

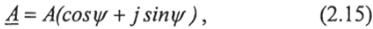
где 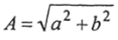 — модуль комплексного числа, равный длине вектора.

ОА; 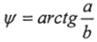— угол, на который вектор О А повернут по отношению к положительному направлению вещественной оси (Яе).

Угол у/ положителен, если он отсчитывается в направлении, противоположном вращению часовой стрелки, и отрицателен, если отсчитывается в направлении вращения часовой стрелки.

Используя формулу Эйлера из (2.15) получим.

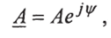
где — поворотный множитель, указывающий, на какой угол по отношению к вещественной оси должен быть повернут вектор, длина которого равна модулю |И|.

Таким образом, поворот вектора ОА на угол ±у/г/2 соответствует умножению его на ± у; поворот на ± у/г — умножению его на -1 и т. д.

Над комплексными числами, изображающими векторы ЭДС, напряжений и токов, можно производить все алгебраические действия:

• Сложение и вычитание чисел:

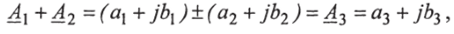
• Умножение чисел:

а)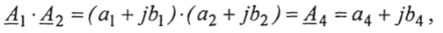

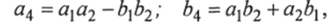
б).

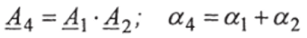
• • Деление чисел:
  • а)

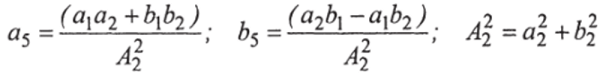
б).

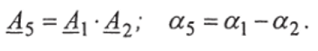
Таким образом, сложение и вычитание чисел лучше производить в алгебраической форме, а умножение и деление — показательной форме.

Представим синусоидальный ток в комплексной форме. Мгновенное значение синусоидального тока.

можно представить вектор тока / в комплексной форме (рис. 2.7):

где l_a -1 cosy/j — вещественная часть комплекса тока (активная составляющая тока); I_b — I 'siruj/i — мнимая часть комплекса тока (реактивная составляющая тока); 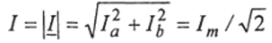 — модуль комплекса тока.

Пример 2.1. Дано мгновенное значение тока:

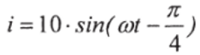
Требуется записать вектор тока в комплексной форме. Решение:

В показательной форме:

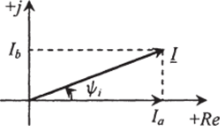
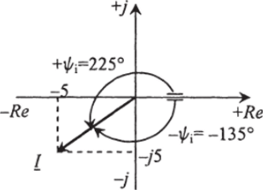
Рис. 2.7. Вектор синусоидального тока на комплексной плоскости Рис. 2.8. Расположение вектора тока /.

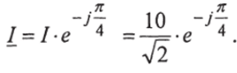
В алгебраической форме:

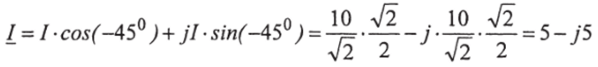
Пример 2.2. Дан вектор тока:

Требуется записать мгновенное значение тока, определить угол у/₍ между вектором / и вещественной осью и изобразить вектор / графически.

Решение:

В общем виде:

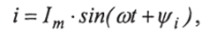
где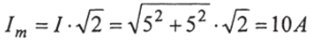

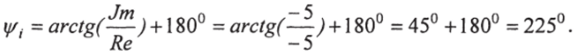
Таким образом мгновенные значения тока и у/₁:

Табл. 2.1. Синусоидальные функции времени в комплексной форме.

На рис. 2.8. приведено расположение вектора / на комплексной плоскости в примере 2.

В табл. 2.1. представлены синусоидальные функции времени в комплексной показательной и алгебраической формах для различных аргументов. Использование этих выражений поможет при решении задач в комплексной форме и проведении различных преобразований комплексных чисел.