Законы распределения случайных процессов

Закон распределения дает практически полную информацию о свойствах и статистических параметрах случайного процесса и позволяет ответить на поставленные вопросы о его поведении во времени.

Нормальный закон распределения

Центральная предельная теорема теории вероятностей определяет условия, при которых реальный случайный процесс приближается к нормальному. Центральная предельная теорема Ляпунова^[1] гласит: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величину влияние каждой из которых на всю сумму ничтожно мало у то X имеет распределение, близкое к нормальному. Это обстоятельство в большой степени объясняет то важное место, которое занимают гауссовские процессы в практике исследований, поскольку для большинства случайных величин выполняются условия теоремы Ляпунова.

Плотность вероятности гауссовского (нормального) случайного процесса имеет вид симметричного колокола, быстро убывающего по мере отклонения от центра. Одномерный нормальный закон распределения плотности вероятности.

На рис. 3.5 показаны графики плотности вероятности нормального закона распределения случайного процесса для трех значений CKO а_г. (при ст_г = 1 плотность вероятности р = 0,4). Функция плотности вероятности р (х — т_х) этого закона является симметричной относительно нуля (или среднего значения — математического ожидания). С увеличением ст_г максимум функции уменьшается, а кривая плотности вероятности становится более пологой относительно оси абсцисс.

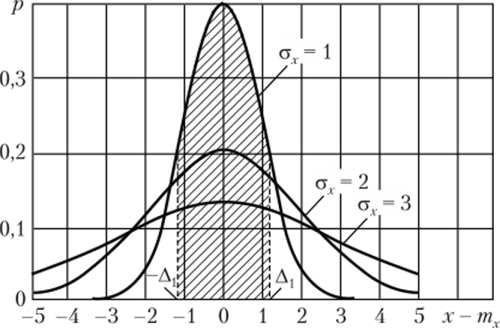
Рис. 35. Графики плотности вероятности нормального закона распределения

Интегральную функцию распределения вычислим как вероятность пребывания случайной величины х в некотором интервале случайных величин (—А, А) (здесь, А = х — т_г — новая переменная). Подставив выражение (3.7) в формулу (3.2), при т_г = 0 получим.

Отметим геометрическую интерпретацию закона распределения (3.8). Па графике плотности вероятности (см. рис. 3.5) для конкретного СКО ст_г и интервала значений (-А, А,) вероятность численно равна площади S заштрихованной фигуры, ограниченной функцией р (х), отрезком оси отА, до А, и ординатами р (-А,), р (А,). Чем шире интервал значений х (-Д, А,), тем больше площадь S, т. е. больше вероятность попадания случайных величин, А в этот интервал. Для интервала (-°о, оо) вероятность Р (-°° < А < оо) = 1. Чтобы удобнее вести анализ процесса и расчеты числовых характеристик, свяжем с СКО ст_г, введя новую переменную у = х/о_х. Тогда функция распределения (3.8) будет.

где г = А/ст,.

Выражение

представляет собой функцию Лапласа, или интеграл вероятности. Эта вероятностная функция хорошо изучена и табулирована.

Нормальный закон распределения, представленный в зависимости от относительного аргумента z = A/a_v, называют нормированным (иногда употребляют термин «стандартный») нормальным законом и задают более простым соотношением.

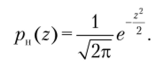
График функции нормированного нормального закона при z = А совпадает с графиком нормального закона (3.8) для СКО ст_г = 1 (см. рис. 3.5). Нормирование нормального закона распределения приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения дифференциальной функции нормированного нормального закона распределения случайных величин сведены в таблицы, которые можно найти в литературе по теории вероятностей и теории случайных процессов.

Интегральная функция нормального закона распределения имеет вид монотонной нечетной симметричной кривой, принимающей значения от пуля до единицы при изменении аргумента х отоо до оо (рис. 3.6).

Рис. 3.6. Интегральная функция нормального закона распределения

Наибольшее число теоретических результатов в статистической теории связи получено применительно к нормальным процессам. Фактически любая многомерная плотность вероятности гауссова случайного процесса определяется двумя характеристиками — математическим ожиданием и функцией корреляции. При негауссовом случайном процессе на входе отыскание закона распределения на выходе цепи является сложной задачей, не имеющей прямого однозначного решения.

• [1] Александр Михайлович Ляпунов (1857—1918) — русский математик и механик.