Максимизация полезности, потребительское равновесие и спрос

Максимизация полезности

Из многочисленных альтернатив потребитель выбирает такие варианты и сочетания благ, которые соответствуют его представлениям о полезности покупок, соизмеренных с возможностями личных денежных доходов, т. е. бюджетных возможностей. Потребительский эффект полезности блага соотносится и сопоставляется покупателем с уплаченными за них деньгами. В данном случае деньги выступают для покупателей важной и достаточно определенной количественной мерой полезности. Другой, нс менее существенной и достаточно определенной, мерой полезности выступает количество благ по данной цене, необходимых для удовлетворения потребности. Каждый покупатель индивидуально и субъективно убеждается, что полезность блага соразмерна с его ценой. В этом случае покупка его первой единицы приносит наибольшее удовлетворение, вследствие чего потребитель осуществит вторую, третью и последующие покупки столь полезного для себя блага. Поскольку будет возрастать и суммарный объем этой полезности, то покупатель, возможно, продолжит закупки. Но будет ли он это делать до бесконечности, наращивая потребление только одного вида благ? Прежде всего потребитель ориентируется на максимизацию полезности благ, закупаемых на данную сумму личного денежного дохода (бюджета). При фиксированном бюджете и постоянных текущих ценах благ потребитель руководствуется правилом: при убывающей предельной полезности благ он стремится максимизировать суммарный полезный эффект, общую полезность осуществляемых покупок. Поскольку оценка полезности неотделима от цеп покупаемых благ, то правило максимизации полезности достигается при следующем условии: равная предельная полезность благ / равновеликая единица денежных затрат.

Когда один из товаров имеет сравнительно большую предельную полезность на единицу денежных затрат, покупатель будет увеличивать его закупку, стремясь максимизировать суммарный потребительский эффект именно этими закупками. Одновременно будет сокращаться закупка благ с меньшей предельной полезностью на такую же единицу денежных затрат. Из расходуемых на покупки денег покупатель сначала может определить среднюю арифметическую величину предельной полезности по каждому из покупаемых благ. Продемонстрируем это с помощью еще одного числового примера (табл. 7.2).

Таблица 7.2. Выбор максимально полезного товара

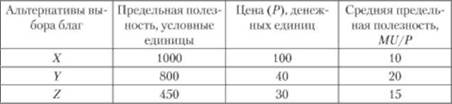
Как видно из табл. 7.2, правило потребительского выбора покупателя, ориентирующегося на максимизацию полезности, выявляет нерациональность расходования денег на товары X и Z, так как наибольшей полезностью обладает альтернативный товар У (его полезность равняется 20). Руководствуясь правилом потребительского выбора, покупатель может достичь равновесия путем замещения менее полезных благ более полезными. Замещение одного блага другим требует соизмерения максимального количества благ, от которых потребитель отказывается ради получения одной дополнительной единицы другого блага. Увеличение полезности от затрат на приобретение блага У должно уравновесить снижение потребления блага X. В конечном итоге такие замещения обеспечивают одинаковый уровень полезности благ на равновеликую единицу денежных затрат. Максимальный потребительский эффект рациональный потребитель соизмерит и с полезностью благ, и с их ценами. Точнее, цены позволяют соизмерить пропорции закупаемых благ. В данном случае покупатель действует по так называемому правилу равных предельных полезностей на единицу своих денежных расходов, согласно которому.

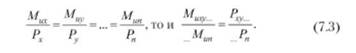
По существу, покупатель перераспределяет свои денежные расходы в пользу большей закупки блага У, отказавшись от последней единицы блага X Цена X, равная в нашем примере 100 денежным единицам, позволит купить дополнительно 2,5 единицы более полезного блага У, что даст более высокий полезный эффект. В денежном выражении он составит 2000 денежных единиц потребления блага У. За вычетом 1000 денежных единиц от экономии на благе X покупатель получает потребительскую выгоду от рационального выбора, равную 1000 денежных единиц полезного эффекта. Уравновесив таким образом свою выгоду и затраты, покупатель достигает равновесия, сбалансированного по правилу равной предельной полезности на равную денежную единицу расходов (табл. 7.3).

Таблица 7.3. Потребительское равновесие (числовой пример)

Максимизация полезности закупок достигается при условии одинаковой предельной полезности на каждую дополнительную единицу денежных затрат. Но соотношение предельной полезности любых благ должно быть уравновешено и их ценами. Рациональный потребитель уравновесит предельную полезность любого блага с предельными денежными затратами из собственного бюджета, руководствуясь правилом, которое можно выразить следующим образом:

где X, У — виды благ; Рг, Ру — цены этих благ; 1 — доход потребителя, его личный бюджет.

Замещения позволяют потребителю не только сопоставлять предельные (дополнительные) выгоды и предельные (дополнительные) затраты, но и достичь их сбалансированного равенства, распределив покупки в соответствии с размерами личного бюджета.