Двойственные оценки в экономико-математическом анализе

Одним из эффективных средств экономико-математического анализа является использование объективно обусловленных оценок оптимального плана. Такого рода анализ базируется на свойствах двойственных оценок.

Известны общие математические и экономические свойства двойственных оценок для задач на оптимум, характерные для задач любой экономической природы [1,2]:

• — оценки как мера дефицитности ресурсов и продукции;
• — оценки как мера влияния ограничений на функционал;
• — оценки как инструмент определения эффективности отдельных вариантов;
• — оценки как инструмент балансирования суммарных затрат и результатов.

Однако экономическая интерпретация этих оценок может быть совершенно различной для разных задач.

Обратимся к конкретной задаче и проиллюстрируем выше перечисленные свойства на примере следующей задачи линейного программирования.

Задача.На кондитерскую фабрику перед Новым годом поступил срочный заказ на подарочные наборы конфет, и были указаны возможные варианты трех наборов: А, В, С. Варианты наборов, их стоимости и имеющиеся товарные запасы конфет на фабрике представлены в таблице 1. Определить оптимальное количество подарочных наборов каждого типа, при котором фабрика обеспечит максимальный доход от продажи.

двойственный оценка минимальный целевой Таблица 1.

Предположим, что производится x1 набора А, x2набора B и x3набора C. Для определения оптимального плана производства нужно решить задачу, состоящую в максимизации целевой функции.

F (x) = 72×1 + 62×2 + 76×3(1).

при следующих условиях:

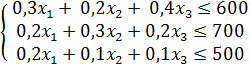
(2).

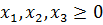
(3).

Припишем каждому из наименования конфет, используемых для составления подарочных наборов, двойственную оценку, соответственно равную y1, y2иy3. Тогда общая оценка конфет, используемых на изготовления подарочных наборов, составит.

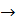
L (y) = 600y1 +700y2 + 500y3min (4).

Согласно условию, двойственные оценки должны быть такими, чтобы общая оценка конфет, используемых на изготовление набора каждого вида, была не меньше цены наборы данного вида, т. е. y1, y2иy3 должны удовлетворять следующей системе неравенств:

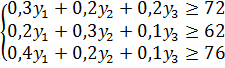
(5).

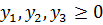
(6).

Как известно, задачи (1)-(3) и (4)-(6) образуют симметричную пару двойственных задач. Решение прямой задачи дает оптимальный план создания подарочных наборов A, В и С, а решение двойственной — оптимальную систему оценок конфет, используемых для создания этих подарочных наборов.

Связь исходной и двойственной задач заключается, в частности, и в том, что решение одной из них может быть получено непосредственно из решения другой.

Реализуя модель задачи (1)-(3) средствами MSExcel, получено оптимальное решение исходной задачи, представленное в таблице 2.

Таблица 2.

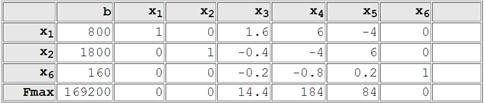
Из данной таблицы видно, что оптимальным планом создания подарочных наборов является такой, при котором получено 800 кг набора типа, А и 1800 кг набора типа В. При данном плане производства остается неиспользованным 160 кг конфет «Красная шапочка», а общая стоимость подарочных наборов равна 169 200 руб. Из таблицы 2 также видно, что оптимальным решением двойственной задачи является.

y1 = 184, y2 = 84, y3 = 0.

Переменные y1и y2обозначают условные двойственные оценки конфет, соответственно «Трюфель» и «Мишка на севере». Эти оценки отличны от нуля, а значит конфеты «Трюфель» и «Мишка на севере» полностью используется при оптимальном плане создания подарочных наборов. Двойственная оценка конфет «Красная шапочка» равна нулю. Этот вид конфет не полностью используется при оптимальном плане производства продукции.

Таким образом, положительную двойственную оценку имеют лишь те виды конфет, которые полностью используются при оптимальном плане создания подарочных наборов. Поэтому двойственные оценки определяют дефицитность используемых фабрикой конфет. Более того, величина данной двойственной оценки показывает, на сколько возрастает максимальное значение целевой функции прямой задачи при увеличении количества конфет соответствующего вида на 1 кг. Так, увеличение количества конфет «Трюфель» на 1 кг приведет к тому, что появится возможность найти новый оптимальный план создания подарочных наборов, при котором общая стоимость подарочного набора возрастет на 184 руб. и станет равной 169 200+184=169 384 руб. При этом числа, стоящие в столбце вектора x4таблицы 2, показывают, что указанное увеличение общей стоимости подарочных наборов может быть достигнуто за счет увеличения выпуска набора, А на 6 ед. и сокращения набора В на 4 ед. Вследствие этого использование конфет «Красная шапочка» возрастет на 0,8 кг.

Точно так же увеличение на 1 кг конфет «Мишка на севере» позволит найти новый оптимальный план подарочных наборов, при котором общая стоимость создаваемых подарочных наборов возрастет на 84 руб. и составит 169 200 + 84 = 169 284 руб. Это будет достигнуто в результате увеличения выпуска набора В на 6 ед. и уменьшения набора, А на 4 ед., причем объем используемых конфет «Красная шапочка» уменьшится на 0,2 кг.