Цикл Карно, теорема Карно. 
Обобщенные и эквивалентные циклы Карно

Наивыгоднейшим теоретическим циклом теплового двигателя, имеющим наибольший термический КПД в заданном температурном интервале, является цикл, предложенный французским ученым Сади Карно. Такой цикл должен состоять из равновесных обратимых процессов, поскольку только в этом случае будут отсутствовать потери энергии, сопутствующие всякому неравновесному процессу. Для получения наибольшего КПД цикла следует выбрать такие равновесные процессы, которые давали бы при расширении рабочего тела наивыгоднейшее преобразование энергии в работу, а при сжатии — наинизшие затраты энергии. В этом случае особое значение приобретают изотермы и адиабаты. Для осуществления обратимого процесса теплообмена достаточно иметь один источник теплоты постоянной температуры, обменивающийся с рабочим телом теплотой при бесконечно малой разности температур. Для адиабатных процессов в связи с отсутствием теплообмена термическая обратимость исключается, а механическая необратимость достигается бесконечно медленным протеканием процесса при бесконечно малой разности давлений между рабочим телом и окружающей средой.

Кроме того, эти процессы являются самыми выгодными с точки зрения получения работы, так как в изотермическом процессе вся сообщаемая теплота полностью превращается в работу, а в адиабатном процессе работа производится только за счет уменьшения запаса внутренней энергии рабочего тела.

Таким образом, для осуществления цикла Карно необходимо иметь всего два источника тепла (теплоотдатчик и теплоприемник), температура которых не изменяется при теплообмене с рабочим телом.

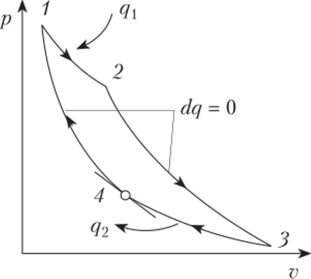
Рис. 5.3. Цикл Карно

Цикл Карно представлен в диаграммах pv и Ts на рис. 5.3. По изотерме 1—2 подводится теплота q_{ при температуре Т_и затем по адиабате 2—3 продолжается расширение рабочего тела, при этом температура снижается до Т₂.

Изотермическое сжатие 3—4 сопровождается отводом теплоты q₂ при температуре Т₂, а затем в результате адиабатного сжатия 4—1 рабочее тело возвращается в первоначальное состояние. Работа в цикле Карно измеряется площадью 1—2—3—4_у ограниченной двумя изотермами и двумя адиабатами.

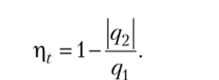
При выводе формулы для термического КПД цикла Карно воспользуемся формулой (5.1).

Находим значения теплоты, подводимой и отводимой в цикле Карно:

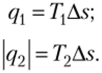
Тогда КПД цикла Карно будет определен как.

Теорема Карно гласит, что термический КПД цикла Карно не зависит от физических свойств рабочего тела, поскольку в формулу, определяющую этот КПД, не входят характеристики, определяющие свойства этого тела.

Анализ формулы (5.4) показывает, что = 1 при Т_] —> °° или Т₂ = О и г)^ =0 при Т_х = Т_2у что подтверждает формулировки второго начала термодинамики.

Цикл Карно на практике неосуществим, так как реальные процессы, протекающие в тепловых двигателях, не являются изотермическими и адиабатными, и выполнить их практически невозможно. Несмотря на это, значение цикла Карно очень велико, поскольку его термический КПД является пределом для данного интервала температур.

Чем ближе при одинаковом интервале температур термический КПД рассматриваемого цикла к термическому КПД цикла Карно, тем совершеннее двигатель.

Если в цикле Карно обратимые адиабатные процессы заменить любыми другими обратимыми эквидистантными (равноотстоящими) кривыми, то получим гак называемый обобщенный цикл Карно (рис. 5.4).

Рис. 5.4. Обобщенный цикл Карно.

Термический КПД такого цикла равен термическому КПД цикла Карно. Достигается это в том случае, если отведенное от рабочего тела в процессе расширения 2—3 количество теплоты q_per подводится к рабочему телу в процессе сжатия 4—1 (возвращается в цикл). Возврат теплоты осуществляется при помощи точечных источников теплоты (dq_per), называемых регенераторами, а процесс возврата теплоты в цикл — регенерацией.

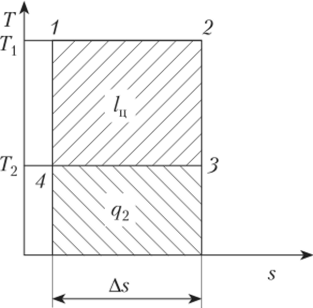
Для сравнения степени термодинамического совершенства циклов различных тепловых двигателей используют понятие об эквивалентном цикле Карно. При этом выражают количество подведенной и отведенной теплоты через их средние термодинамические температуры.

Средней термодинамической (или среднеинтегральной) температурой называют условную постоянную температуру, при которой в одинаковом интервале энтропий участвует такое же количество теплоты, что и при переменной температуре (рис. 5.5).

Рис. 5.5. Средняя термодинамическая температура.

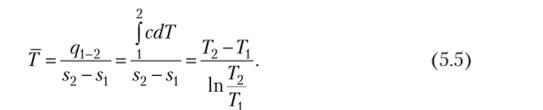
Рассчитывая для произвольного цикла 1—2—3—4 средние термодинамические температуры подвода и отвода теплоты (рис. 5.6) как или.

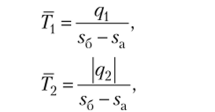
где s_a, s₆ — значения удельной энтропии для точек а и б соответственно, определим формулу для термического КПД этого цикла:

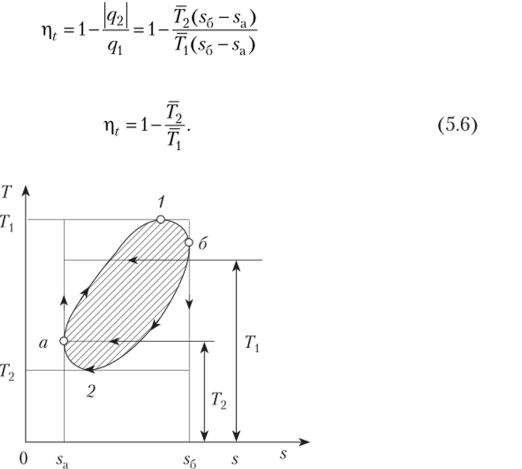
Рис. 5.6. Эквивалентный цикл Карно.

Эквивалентный цикл Карно эквивалентен данному циклу по величине работы и эффективности превращения теплоты в работу и представйм в виде прямоугольника с изотермами 7j и Т₂ и адиабатами s_a = const и Sg = const.

Из рис. 5.6 следует, что термический КПД цикла Карно больше КПД любого иного цикла, осуществляемого в тех же пределах температур. Действительно, поскольку Т > Т_ь а Т₂ > Т₂, то тр^к > тр.