Результаты исследования и их обсуждения

Влияние ТРИАР-массажа на функциональное состояние сердечно-сосудистой системы пациентов с ишемическим инсультом

Показатели сердечно-сосудистой системы оценивались при помощи пробы Руфье, которую проводили до и после реабилитации в контрольной и основной группах.

Таблица 3.1 — Результаты оценки пробы Руфье у пациентов с ишемическим инсультом в контрольной группе.

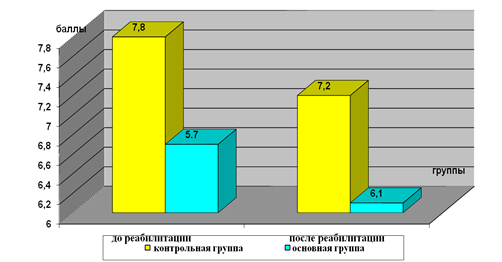
Рисунок 3.1.1 — Результаты пробы Руфье у пациентов с ишемическим инсультом Из таблиц 3.1 и рисунка 3.1.1 видно, что после проведения реабилитационных мероприятий показатели пробы Руфье имели положительную динамику как в основной группе: показатель сердечной деятельность сократился с 7,8 (± 0,7) до 5,7 (± 0,6), так и в контрольной группе с 7,2 (±1) до 6,1, (± 0,9).

Данные результаты свидетельствуют об эффективности ТРИАР-массажа, так как под ее воздействием у пациентов экспериментальной группы произошло достоверное улучшение состояния сердечно — сосудистой системы. Улучшение эмоционального состояния пациентов экспериментальной группы объясняется тем, что при ТРИАР-масаже происходит рефлекторный выброс нейропептидов — эндорфинов и энкефалинов (своеобразных опиатов человеческого организма), которые обладают обезболивающим и поднимающим настроение действием. Происходит активизация кровои лимфообращения как в обрабатываемой анатомической области, так и во всём организме, и, как следствие, ускорение общего обмена веществ. Выброс эндорфинов приводит к значительному улучшению настроения, чувству психологического комфорта и устранению напряженности в межличностных отношениях.