Проверка гипотезы о равенстве дисперсий

Предположим, что у нас имеются две независимые выборки объемами т и п соответственно: (х_{, х₂,…, х_т) из ГС, имеющей распределение N (a_{ya^)_y и (г/_1? у₂,у_п) из ГС, имеющей распределение N (a₂,<5).

Необходимо проверить гипотезу о равенстве дисперсий, т. е. Я₀ <�з =а^. Так как выборки независимы и выбраны из ГС, распределенных нормально, то из леммы о F-распределении следует, что т. е. представляет собой F-отношение. Но если гипотеза Я₀ верна, т. е. 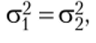то получаем, что 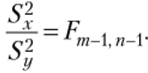Следовательно, в качестве статистики критерия можно взять отношение исправленных дисперсий. Для определенности берут отношение максимальной дисперсии к минимальной. Обозначим.

тогда.

Если гипотеза Я₀ верна, то D = F_ku. т. е. представляет собой Е-отношение; при этом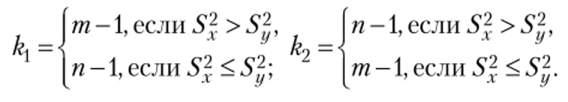

Теперь мы должны построить критическую область для критерия D. В силу специфики^{-распределения} за критическую область принимаются два интервала: интервал, удовлетворяющий неравенству F^^ >F₂, и интервал, удовлетворяющий неравенству 0 < Е^ ^ <�Р, причем критические точки подбираются так, чтобы 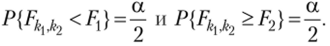Таким образом, критическая область К_а = {D: D < Е, D > F->). Левую критическую точку^{-распределения} можно выразить через правую критическую точку F^ -распределения. Действительно, Таким образом, необходимо найти только правые критические точки для F_k ^ и Е^, чтобы определить Е, и Е₂, причем Е, = 1/Е_к._р(а/2, k₂,/,), Е, = Е_кр(а/2, k_x, k₂).

Далее по реализациям выборок, используя статистику (9.6), вычисляем D_mбл. Если окажется, что D_Ha6jI е (Ер Е₂), то гипотеза Н₀ согласуется с экспериментальными данными. Если же Я_иабл g (Ер Е₂), то гипотеза #₀ отвергается.

Пример 9.4. На предприятии разработаны два метода изготовления изделия. Чтобы проверить, одинаково ли в среднем тратится сырья на изготовление изделия обоими методами, собраны статистические данные о расходе сырья на единицу готовой продукции в процессе работы обоими методами:

Предполагая, что выборки независимы и взяты из нормально распределенных ГС с параметрами N (a_v о²) и N (a₂, о₂) соответственно, проверим гипотезу о равенстве средних, т. е. Я₀: а, = а₂.

Решение. Так как дисперсии неизвестны, то вначале проверим гипотезу о равенстве дисперсий: Н₀:а?=а₂. В нашем случае Х = 2,5, у =3,3, S² =0,1, 5;; =0,245, S²

Дибл =-| = 2,45, а = 0,05, k_{ = 4, k₂ = 5.

&#X

По таблице критических точек Е-распределения находим Е₍ = 1/Е_К|,(0,025,5,4) = = 0,1068, Е₂ = Е_кр(0,025, 4, 5) = 7,3879. Так как ?)_набл е (0,1068; 7,3879), то гипотеза Н₀ принимается.

Теперь, учитывая, что дисперсии равны, проверим гипотезу II_Q: а_л = а₂. Имеем.

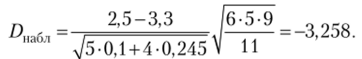aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Для, а = 0,05 при k = m+n-2 = 9 находим Так как |Д_|а6л| > 2,2622, то гипотеза 7/₀ отвергается.

Таким образом, на изготовление изделия двумя методами тратится в среднем разное количество сырья.