Понятие о расчете пространственных рам

При расчете пространственных рам методом перемещений за неизвестные принимаются, так же как и для плоских рам, угловые перемещения жестких узлов и независимые линейные перемещения всех узлов рамы. Так как в пространственной системе каждый жесткий узел может иметь повороты в трех взаимно перпендикулярных плоскостях, степень кинематической неопределимости в этом случае будет определяться по формуле.

где — число жестких узлов расчетной схемы, способных к повороту при ее деформации; п_л — степень линейной подвижности всех узлов схемы, определяемая как степень свободы шарнирного механизма, получаемого из заданной схемы рамы путем введения во все ее узлы сквозных шарниров:

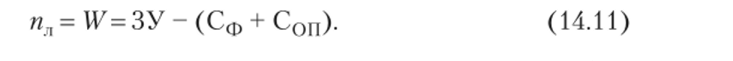
Для получения основной системы во все жесткие узлы рамы необходимо ввести пространственные «плавающие» защемления, препятствующие повороту узлов относительно трех координатных осей, и линейные связи, не допускающие линейных перемещений узлов. В общем случае в «плавающих» защемлениях возможно возникновение трех реактивных моментов, а в линейных связях — линейных реактивных сил.

Например, для рамы, изображенной на рис. 14.26, а, степень кинематической неопределимости п_к = п_у + п_л = 3- 4 + 4 = 16. Основная система для этой рамы представлена на рис. 14.26, 6.

Канонические уравнения метода перемещения для пространственных рам имеют тот же вид, что и для плоских.

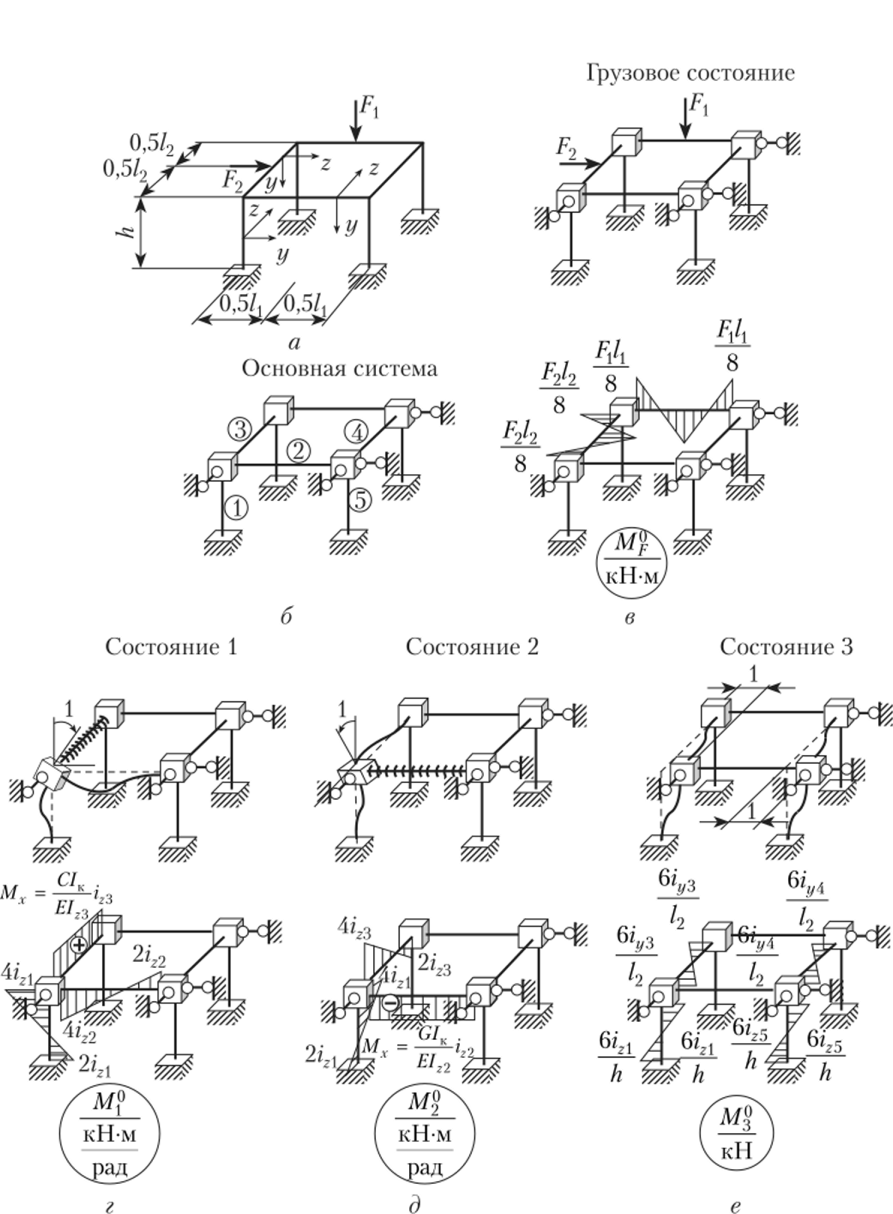
Рис. 14.26.

Для определения коэффициентов при неизвестных и свободных членов канонических уравнений строятся эпюры изгибающих моментов от единичных принудительных смещений дополнительных связей и действия внешней нагрузки. Построение эпюр изгибающих моментов, выполняемое с использованием таблиц реакций (см. прил. 10 и 11), было показано при расчете плоских рам. При принудительном повороте дополнительных угловых связей в некоторых стержнях основной системы необходимо учитывать их кручение. Значения крутящих моментов от единичного поворота угловой связи определяются на основании (9.12) при ср = 1.

где i — относительная жесткость относительно какой-либо оси поперечного сечения стержня, выбранная в качестве общего множителя при расчете; EI — изгибная жесткость стержня относительно той же оси (/' = EI / Г).

Для рассматриваемой рамы эпюра Мрот внешней нагрузки показана на рис. 14.26, в, а деформированные состояния основной системы и соответствующие им эпюры моментов Mf, М% и МЦ от двух единичных поворотов во взаимно перпендикулярных плоскостях и одного линейного смещения, соответственно, на рис. 14.26, г — е.

Значения реакций в дополнительных связях определяются на основании уравнений равновесия (2.36) и (2.38) для вырезанной угловой связи или части основной системы.

Эпюры изгибающих моментов в заданной расчетной схеме после определения неизвестных метода перемещений определяются на основании принципа независимости действия сил:

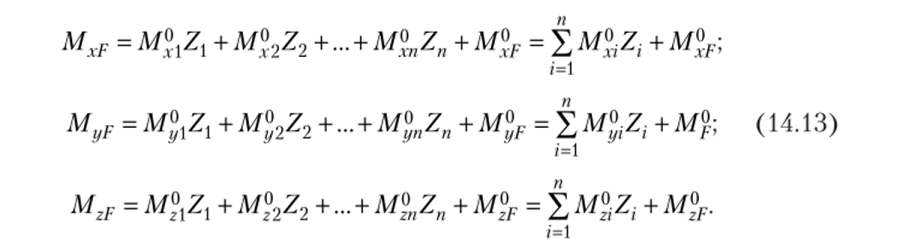
Эпюры поперечных и продольных сил строятся так же, как и при расчете пространственных рам методом сил. На отдельных этапах расчета выполняются те же проверки, что и при расчете плоских рам. Основными и достаточными являются деформационная и статические проверки расчета.

Пример 14.9.

Требуется построить эпюры усилий для пространственной рамы, изображенной на рис. 14.27, а при GI_K/EI = 0,5 и I_z = I_y = I. Действующая нагрузка: F= 106 кН, q = = 29 кЫ/м.

Относительные жесткости стержней рамы:

• — стержней ЛВ и BE — ц = EI/A = i;
• — стержня BD — i₂ = 2 ?7/4 = 2/;
• — стержня ВС— /₃ = 4EI/A = Ai.

Решение. 1. Степень кинематической неопределимости п_к = 3, так как узел В не имеет линейных смещений. Основная система метода перемещений показана на рис. 14.27, 6.

При заданной нагрузке, действующей в двух взаимно перпендикулярных плоскостях, угол поворота в третьей плоскости, перпендикулярной плоскостям действия нагрузки, = 0.

2. Следовательно, канонические уравнения метода перемещений будут иметь вид.

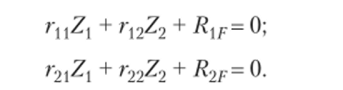
Так как перемещения Zj и Z₂ возможны в двух взаимно перпендикулярных плоскостях и независимы друг от друга, в приведенных уравнениях коэффициенты г₁₂ = = г₂ = 0, то уравнения примут вид.

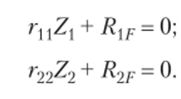
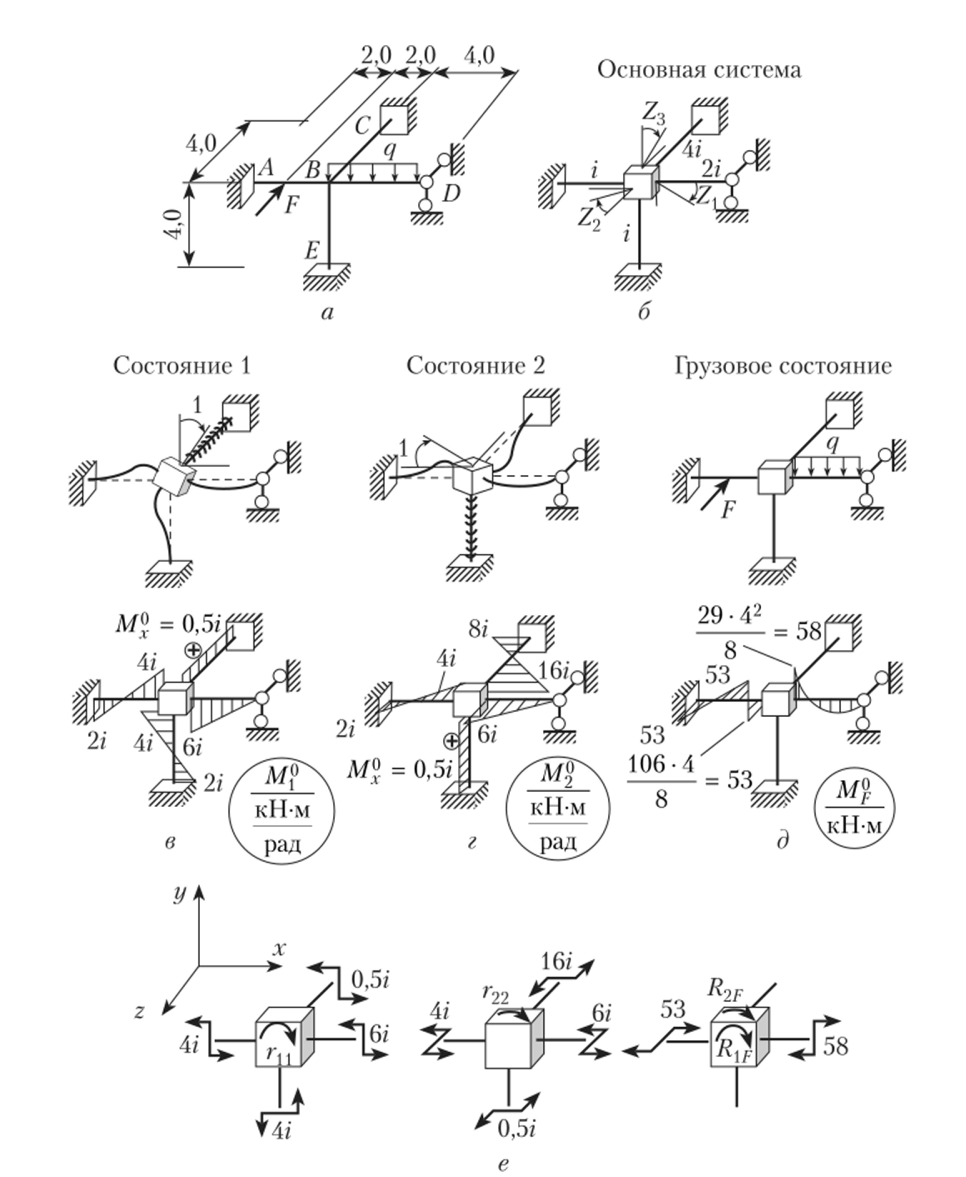
Рис. 14.27.

• 3. Деформированные схемы основной системы от принудительных поворотов дополнительных связей на угол, равный единице, и соответствующие ей эпюры М^] и М$ (рис. 14.27, в_у г) строим с использованием нрил. 10.
• 4. Эпюру М}! в основной системе от действия внешней нагрузки (рис. 14.27, д) строим с использованием нрил. 11.
• 5. Реакции в дополнительной связи во всех расчетных состояниях определены по рис. 14.27, г следующим образом:

zLM₂ = 0; г_{{ {} — 4/ - 4/ - б/ - 0,5/ = 0, г, = 14,5/ кН м/рад;

1 М_У = 0; г₂₂ — 4/ -16/ - 6/ -0,5/ = 0, >22 = 26,5/ кН м/рад;

YjM₂ = 0; R_[F + 58 = 0, R_F= «58 кН м;

• 1 М_у = 0; R_2F + 53 = 0, R_2F= -53 кН м.
• 6. Запишем канонические уравнения в численном виде:
• 14,5/Z, — 58 = 0,
• 26,5iZ₂ — 53 = 0,

откуда Zj =58 / 14,5/ = 4 / / рад; Z₂ = 53 / 26,5/ = 2 / / рад.

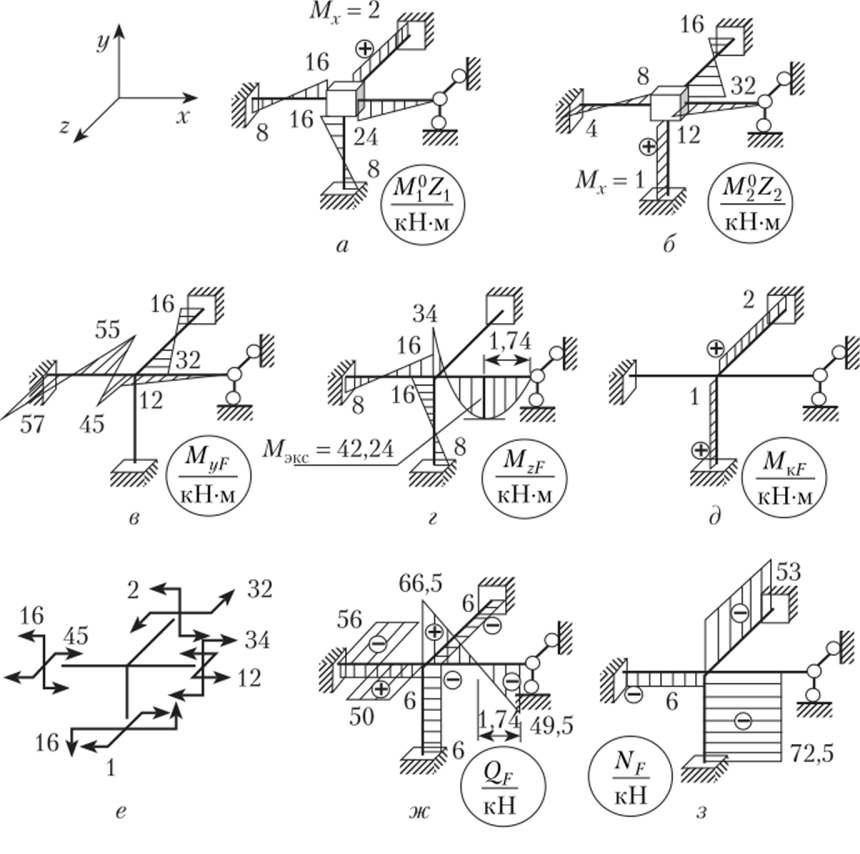
FUC. 14.^о.

• 7. Эпюру изгибающих моментов в заданной схеме рамы будем строить по формуле M_F = M_{ + M₂Z₂ + М?. Слагаемые приведенной формулы и результат сложения приведены на рис. 14.27, д и 14.28, а, 6. Результат сложения, эпюру M_F, для наглядности представим в виде суммы трех эпюр М_у, М₂ и М^= М_к (рис. 14.28, в — д) в общей системе координат xyz.
• 8. Проверка равновесия жесткого узла, но полученной эпюре M_F показана на рис. 14.28, е.
• 9. Эпюры Q_f и N_f приведены на рис. 14.28, ж, з.