Устойчивость арок, колец, пластин, оболочек и потеря плоской формы изгиба

В результате изучения данной главы студент должен: знать

• • основы расчета криволинейных стержней на устойчивость;
• • основы расчета стержней в случае потери плоской формы изгиба; уметь
• • рассчитывать на устойчивость арки с помощью таблиц Динника;
• • решать элементарные задачи устойчивости пластин и оболочек; владеть
• • анализом форм потери устойчивости арок;
• • расчетом арки на основе программных комплексов типа ЛИРА.

Устойчивость круглого кольца

Криволинейные стержни встречаются повсеместно в машиностроении, а также в строительстве, где они в виде арки как несущей конструкции играют большую роль. Очертания арки могут быть разнообразными. Криволинейные стержни и арки, как и прямолинейные стержни, при определенных грузовых воздействиях тоже могут терять первоначальную форму равновесия. Трудоемкость расчета арок существенно зависит от ее формы. Наиболее простым является расчет криволинейных стержней кругового очертания.

Большое практическое значение имеет задача устойчивости кругового кольца, находящегося под действием радиальной нагрузки, равномерно распределенной вдоль окружности (рис. 12.1).

Обозначим через q силу, приходящуюся на единицу длины окружности. Составим уравнения равновесия элемента длиной dy (рис. 12.2). Продольная сила N считается положительной при сжатии.

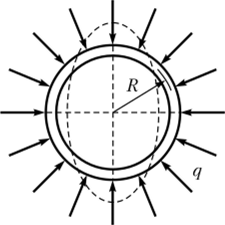
Рис. 12.1. Кольцо под действием радиальной нагрузки.

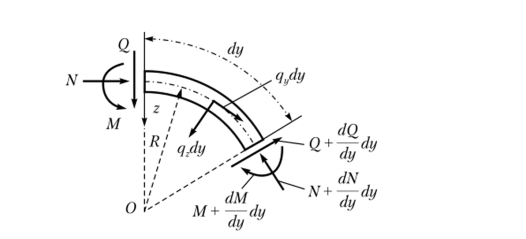
Рис. 12.2. Дифференциальный элемент круглого кольца.

Определим проекции сил на направления касательной и нормали к оси кольца и составим сумму моментов относительно центра круга [41:

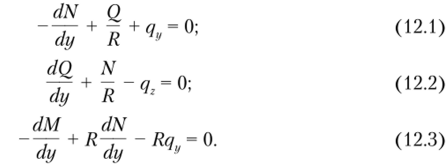
Координата у отсчитывается вдоль дуги, z — к центру; q и q_z — проекции внешней нагрузки на соответствующие направления. Используя необходимые подстановки уравнений (12.1)—(12.3), получим.

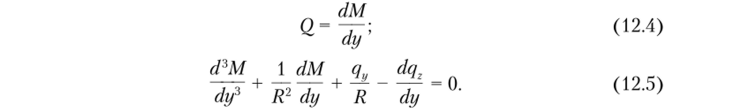
До момента выпучивания кольца.

Изменение кривизны выражается через прогиб w следующим образом:

Первый член в этом выражении такой же, как и в случае прямой балки, второй член находится по рис. 12.3 с учетом изменения радиуса кривизны:

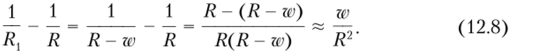
Момент М равен.

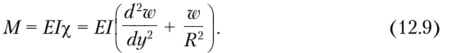
Подставляя это выражение в уравнение (12.5), получим дифференциальное уравнение для перемещения w.

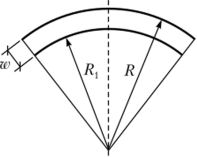
Рис. 12.3. К определению кривизны изогнутой линии.

В задачах устойчивости нужно учесть радиальную составляющую усилий N, возникающую при выпучивании кольца:

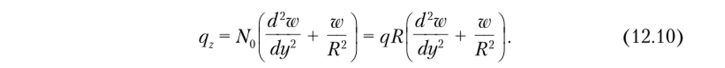
Считая q_y = 0, получим окончательное дифференциальное уравнение.

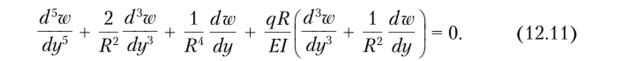
Примем для w выражение.

где п — число полных волн, образующихся по окружности. При п = 1 получим перемещение кольца как твердого тела. Подставляя выражение (12.12) в уравнение (12.11) и считая, что / Ф 0, приходим к следующей зависимости:

Минимальная критическая нагрузка q соответствует двум волнам по окружности (п = 2) и равна При этой нагрузке кольцо превращается в эллипс (см. штриховую линию па рис. 12.1).