Дисперсия генеральной совокупности неизвестна

Пусть X — случайная величина, имеющая нормальный закон распределения, причем математическое ожидание и генеральная дисперсия неизвестны (например, в случае малого объема выборок, п 30). По данным наблюдения находят выборочную среднюю и выборочную исправленную дисперсию, которая является только оценкой неизвестной генеральной дисперсии. Поэтому в качестве проверки нулевой гипотезы принимают критерий (имеющий распределение Стьюдента), ориентированный на малые выборки.

где S— выборочное исправленное среднее квадратичное отклонение.

Критическая область строится в зависимости от типа альтернативной гипотезы:

а) Н. М (Х)*а₀ — критическая область двусторонняя, задаваемая неравенством |К]>ЛТкрпр (/Гкрпр>0). Критическая точка K_Kr«?(aJ) находится по таблице прил. 5 распределения Стьюдента, где а (помещен в верхней строке таблицы) — уровень значимости для двусторонней критической области, /= п-1 — число степеней свободы. Если |К_1и6л | < К*, п_Р ~ нулевая гипотеза принимается, а если Кнабл^^крпр ^- нулевая гипотеза отвергается (признается правильной гипотеза Нi);

• б) Ну. М (Х) > а₀ — критическая область правосторонняя и определяется неравенством К>К_Щ,_ф, где К_Щ1П[1 ищуг в таблице прил. 5 по уровню значимости а (помещен в нижней строке таблицы) для односторонней критической области и числу степеней свободы /=и-1. Если А'"аб,^<А'_Кр пр — нулевая гипотеза принимается, если ^набл^>К"р кр—нулевая гипотеза отвергается (признается гипотеза tfi);
• в) Ну: М (Х)<�а₀ — критическая область левосторонняя, заданная

неравенством К<�К_Щ, _пр (К*_{р пр}<0), где Кщ, щ, находят в таблице прил. 5 по уровню значимости а (помещен в нижней строке таблицы) для односторонней критической области и числу степеней свободы /=л-1, а затем следует взять найденное значение со знаком «минус», приняв = Ккрлса • Если К_юЪ > _лсв — нулевая гипотеза принимается, если К_тgp < _лев, то нулевая гипотеза отвергается.

Пример 9.12. По результатам медицинских наблюдений минимальное среднее динамическое давление крови больных, перенесших операцию сердца с применением 1-го способа анестезии, равно а₀ = 66,9 мм рт. ст. На основе случайной выборки из 10 больных, перенесших аналогичную операцию с применением 2-го способа анестезии, определили х_в = 73,2 мм рт. ст. и У = = 14,4 мм рт. ст. Предполагая, что значения давления крови у подобных больных распределены по нормальному закону, при уровне значимости, а = 0,05 оценить, влияет ли способ анестезии на минимальное среднее динамическое давление крови больных?

Решение. Найдем число степеней свободы f = «-1 = 10−1=9.

Сформулируем нулевую и альтернативную гипотезы.

Н₀: М (Х) = а₀; здесь а₀ = 66,9. Я: М (Х) * а₀; здесь а₀ = 66,9. По формуле (9.5) наблюдаемое значение критерия.

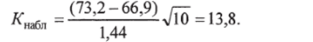
Альтернативная гипотеза имеет вид М (Х) * а₀, поэтому критическая область двусторонняя. По таблице прил. 5 для двусторонней критической области при уровне значимости, а = 0,05 (помещен в верхней строке) и по числу степеней свободы f = 9 найдем критическую точку/^крпр (0,05,9)=2Д6. Так как |Я',_|1бл|=13,8>2,26= «Якр _пр, то нулевую гипотезу Но отвергаем и делаем вывод, что минимальное среднее динамическое давление крови больного зависит от выбора способа анестезии.