Движение сингулярностей в потоках Риччи

Для моделирования изменения метрики при движении сингулярностей используем потоки Риччи [34−41], которые описываются уравнением.

(22).

Здесь — коэффициент диффузии, которые в стандартной теории [34−41] полагают равным, однако в метрике (2) следует положить, тогда (5) сводится к системе уравнений параболического типа:

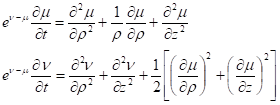
(23).

Сравнивая (23) и (5) находим, что для установившихся потоков при условиях система (23) сводится к (5). Обоснованием для такого перехода от статической системы (5) к системе уравнений параболического типа (23) может служить теория, развитая в работах [34−41] и других, а также теория геометрической турбулентности [42−43].

Физический смысл расширения статической модели (5) до модели (23), описывающей потоки Риччи, заключается в том, что по начальным и граничным условиям можно определить к каким решениям сходится решение системы уравнений (5), содержащее особенности, например, решение (9).

С точки зрения теории Эйнштейна и Инфельда [5−6], движение частиц в потоках Риччи равносильно нулевому приближению, при котором частицы движутся свободно, создавая гравитационное поле. В следующем приближении между частицами возникает сила взаимодействия, которая изменяет параметры движения и т. д. Однако для многих практически важных задач, таких как слияние черных дыр [17−22], достаточно будет знать, как изменяется метрика бинарной системы при сближении центров гравитации с заданной скоростью. Модель потоков Риччи (23) позволяет ответить на этот и другие вопросы, связанные с изменением метрики.

Рассмотрим задачу об установлении потенциалов системы (23) в прямоугольной области.

при заданном начальном условии.

Тем самым можно получить оценку величины второго потенциала для системы тел. Решение будет зависеть от краевых условий, которые мы сформулируем следующим образом:

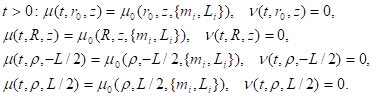
(25).

Здесь — граница области, отделяющая область численного интегрирования от оси системы, содержащей сингулярные точки потенциала (9). Такая постановка задачи позволяет исключить сингулярности в решениях для второго потенциала системы, что, в свою очередь, дает возможность оценить малый параметр .

На рис. 3−5 представлены результаты моделирования установления потенциалов в потоках Риччи, выполненные по (23), (24) и (25) при следующих значениях параметров:

(26).

В этом примере 7 сингулярностей распределены случайным образом на оси системы. На рис. 3−4 показан процесс установления потенциалов в различных точках, указанных над рисунками. На рис. 5 представлены линии уровня функции — модуля отношения потенциалов, в различные моменты времени, указанные над рисунками. Из приведенных данных следует, что потенциалы системы стремятся в каждой точке к некоторым значениям, а модуль отношения потенциалов нигде не превышает 0.0008, т. е. условие действительно выполняется. Отметим, что данные (26) являются типичными для звездных систем с параметрами Солнечной системы.

Рис. 3. Зависимости функции от времени в различных точках (координаты точек указаны над рисунками) в системе, состоящей из семи сингулярностей с суммарной массой

На рис. 6. представлены результаты расчетов модуля отношения потенциалов в различные моменты времени, указанные над рисунками выполненные по (23), (24) и (25) при следующих значениях параметров:

(27).

Рис. 4. Зависимости функции от времени в различных точках (координаты точек указаны над рисунками) в системе, состоящей из семи сингулярностей с суммарной массой

Из сравнения данных на рис. 5 и 6 следует, что при увеличении суммарной массы системы на порядок модуль отношения потенциалов также возрастает на порядок. Из приведенных на рис. 6 данных следует, что модуль отношения потенциалов нигде не превышает 0.01, т. е. условие выполняется и в этом случае.

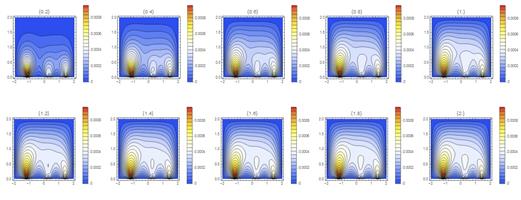
Рис. 5. Линии уровня функции — модуля отношения потенциалов, в различные моменты времени в задаче с данными (26): значения параметра времени указаны над рисунками.

Рис. 6. Линии уровня функции — модуля отношения потенциалов, в различные моменты времени в задаче с данными (27): значения параметра времени указаны над рисунками.

Следовательно, система уравнений (23), описывающая потоки Риччи, позволяет смоделировать гравитационные потенциалы системы многих тел при заданном их положении. В частности, например, можно задать движение сингулярностей и определить возникающие при этом движении гравитационные волны [17−18]. Другое применение теории потоков Риччи было указано в работе [22], где была определена плотность материи, возникающей при столкновении сингулярностей.

Представляет интерес также определение потенциалов при орбитальном движении тел. Для этого достаточно будет предположить, что все тела движутся в одной плоскости из некоторого начального положения на оси симметрии с составляющей скорости перпендикулярной оси. Тогда систему уравнений (23) можно использовать для оценки релятивистских эффектов, обусловленных движением сингулярностей. Однако решение этой задачи выходит за рамки настоящей работы.