Комплексная амплитуда гармонического сигнала

Для гармонического сигнала (тока или напряжения) комплексная амплитуда равна.

. (1.10).

Комплексная амплитуда является комплексным числом (- мнимая единица) и определяется только амплитудой и начальной фазой сигнала и не зависит от его час;

тоты. Комплексная амплитуда обозначается тем же символом, что и амплитуда сигнала, но с точкой сверху.

Например, если мгновенное значение гармонического напряжения равно В, то его комплексная амплитуда равна В или В.

Если запись сигнала отличается от формы (5.1) то необходимо провести соответствующие тригонометрические преобразования, представленные в табл. 1.2.

Таблица 1.2.

Если гармоническое напряжение имеет вид мВ, то после преобразования получим мВ, а комплексная амплитуда будет равна мВ.

Операции с комплексными числами

Комплексные числа могут быть записаны в двух формах: алгебраической и показательной. В алгебраической форме комплексное число (точка сверху используется для обозначения комплексной амплитуды сигнала, а если речь идет о комплексном сопротивлении или проводимости, то используется подчеркивание символа) записывается в виде.

(1.12).

где — действительная, а — мнимая части комплексного числа, — мнимая единица.

В показательной форме комплексное число представляется выражением.

(1.13).

величину называют модулем, а — аргументом комплексного числа. От алгебраической формы можно перейти к показательной, модуль комплексного числа равен.

(1.14).

а аргумент.

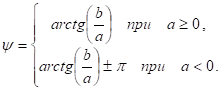
(1.15).

Аргумент комплексного числа, как и начальная фаза гармонического сигнала, величина многозначная, к ней можно добавить (или вычесть) любое число раз. Для обеспечения однозначности аргумента комплексного числа его значения выбирают в диапазоне, например, от до или от 0 до .

Показательную форму комплексного числа можно заменить алгебраической с помощью соотношений.

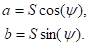
(1.16).

Они вытекают из известной в математике формулы Эйлера,.

(1.17).

Например, если комплексное число в алгебраической форме равно, то в показательной форме его можно записать в виде.

.

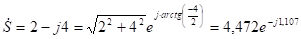
Если комплексное число равно, то в показательной форме получим.

.

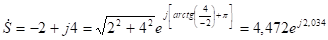
Для комплексного числа в показательной форме в виде его алгебраическая форма имеет вид.

.

С комплексными числами проводятся все четыре арифметические действия.

При сложении и вычитании комплексных чисел и в алгебраической форме получим.

. (1.18).

Если числа заданы в показательной форме, то перед сложением или вычитанием их необходимо преобразовать в алгебраическую форму.

Операции умножения и деления удобнее выполнять в показательной форме, когда и, при этом при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

(1.19).

а при делении делятся модули и вычитаются аргументы числителя и знаменателя.

. (1.20).

Умножение можно провести и с алгебраической формой сомножителей по известным правилам с учетом того, что :

. (1.21).

При делении комплексных чисел в алгебраической форме используется операция устранения комплексности в знаменателе путем умножения числителя и знаменателя дроби на число, комплексно сопряженное знаменателю. Для заданного числа комплексно сопряженное число равно, то есть отличается от противоположным знаком при мнимой части. Произведение двух комплексно сопряженных чисел всегда равно квадрату их модуля,.

. (1.22).

Тогда при делении в алгебраической форме получим.

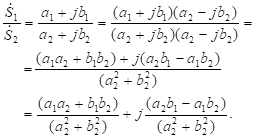
(1.23).

Рассмотрим пример и, тогда.

.

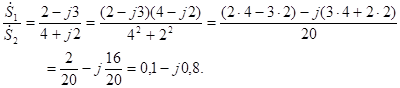
Эти операции можно провести и в показательной форме.

.

.

.

.

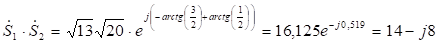
Как видно, полученные результаты совпадают.

Полезно запомнить следующие равенства (табл. 1.3.), вытекающие из формулы Эйлера,.

(1.24).

Таблица 1.3.

Вычисления с комплексными числами удобно проводить на персональной ЭВМ с помощью пакета программ MathCAD.