Понятие о матрицах влияния

В этой треугольной матрице, так же как и в предыдущем примере, строки состоят из ординат линий влияния моментов, а столбцы содержат ординаты эпюр моментов при неподвижном грузе Р = 1, приложенном в точках 1, 2, 3 и 4. В связи со все большим распространением компьютеров удобно пользоваться матричным исчислением, позволяющим легко механизировать все расчеты и составлять для этой цели алгоритмы… Читать ещё >
Понятие о матрицах влияния (реферат, курсовая, диплом, контрольная)
В связи со все большим распространением компьютеров удобно пользоваться матричным исчислением, позволяющим легко механизировать все расчеты и составлять для этой цели алгоритмы и программы.
Матрицами влияния называются таблицы, составленные в определенном порядке из ординат линий влияния како;
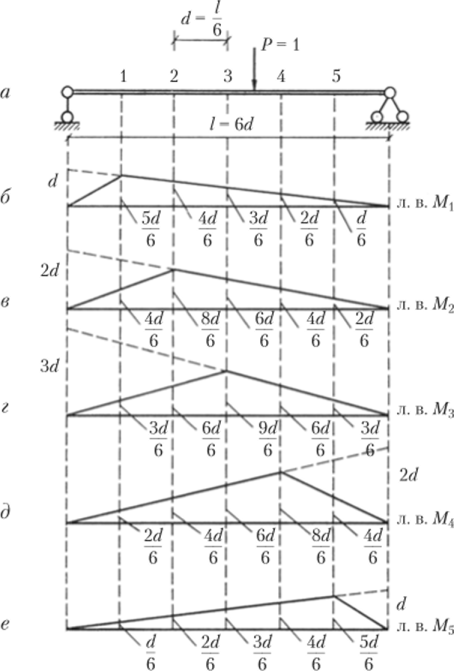
Рис. 2.14.
го-либо фактора. В отличие от линии влияния, позволяющей определить какое-либо усилие при любой нагрузке, матрица влияния применяется для одновременного определения нескольких усилий.
Рассмотрим методику составления матрицы влияния моментов для простой балки. Разобьем балку на шесть равных частей и наметим узловые точки 1, 2,5 (рис. 2.14, а). Изгибающие моменты на опорах равны нулю. А для всех точек, расположенных в пролете, ординаты линий влияния моментов (рис. 2.14, б — е) отличны от нуля. В первой строке матрицы поместим пять ординат л. в. М, располагая их последовательно для точек 1, 2,…, 5. Ординаты л. в. М2 расположим во второй строке. Далее последовательно образуем строки из ординат линий влияния моментов М3, М4 и М5. В результате получим матрицу влияния моментов.
Вынеся за скобку общий множитель (1/6 = //36, получим матрицу с данным общим множителем.

Данная матрица обладает рядом интересных свойств: 1) строки матрицы состоят из ординат линий влияния моментов; 2) столбцы матрицы состоят из ординат эпюр моментов от груза Р = 1, неподвижно приложенного в точках 1, 2,…, 5.
Составим теперь матрицу влияния моментов для балки, заделанной одним концом. Разобьем балку на четыре равные части (рис. 2.15, а). Линии влияния для четырех узловых точек изображены на рис. 2.15, б — д. В точке 5 изгибающий момент при любом положении единичной силы равен нулю, поэтому она не рассматривается. У всех ординат линий влияния имеется общий множитель d = ¼.
Применив описанный выше прием и вынеся за скобку общий множитель //4, получим.

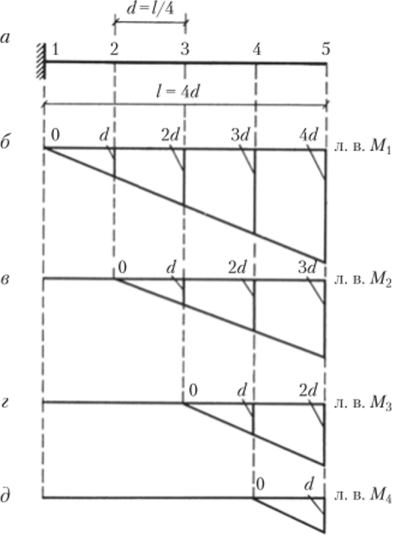
В этой треугольной матрице, так же как и в предыдущем примере, строки состоят из ординат линий влияния моментов, а столбцы содержат ординаты эпюр моментов при неподвижном грузе Р = 1, приложенном в точках 1, 2, 3 и 4.
Таким же способом можно построить матрицы влияния поперечных сил. При этом надо учитывать: 1) узловую передачу нагрузки; 2) особенность, заключающуюся в том, что когда груз совпадает с точкой, определяющей заданное сечение, линия влияния имеет две ординаты. Возникает вопрос, какую из двух ординат включить в матрицу влияния поперечных сил. Ответ на этот вопрос зависит от того, какое из двух сечений, принадлежащих узлу, будет рассматриваться. Если сечение провести в непосредственной близости от узла к, т. е. несколько левее (правее), то в матрицу влияния следует включать ординату, принадлежащую левой (правой) прямой.