Приближенное вычисление корней системы линейных уравнений прямым (точным) и приближенными (итерационными) методами. 
Сравнение методов

Вариант 4.

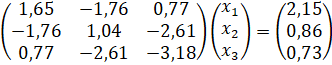
Цель работы: изучение точных и приближенных методов вычисления корней системы нелинейных уравнений Ax = f. Получение навыков решения задач вычислительной математики на ЭВМ. Освоение умения анализировать результаты, полученные на компьютере и сравнивать методы.

Задание: Написать программу вычисления приближенного решения системы линейных уравнений Ax = f с точностью = 10^-5 методом Гаусса. Написать программу вычисления приближенного решения той же системы линейных уравнений Ax = f с точностью = 10^-5 методом наискорейшего спуска и методом сопряженных градиентов. Составить таблицу сходимости метода.

Решение:

Метод Гаусса.

Прямой ход метода:

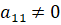
1-й шаг. Предположим, что. Поделим, первое уравнение на этот элемент, который назовем ведущим элементом первого шага:

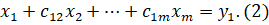
Остальные уравнения системы (1) запишем в виде:

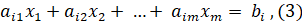
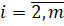
где .

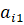
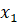
Уравнение (2) умножаем на и вычитаем из i-го уравнения системы (3). Это позволит обратить в нуль коэффициенты при во всех уравнениях кроме первого.

Получим эквивалентную систему вида:

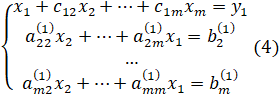
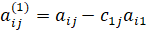
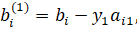
где. Система (4) имеет матрицу вида:

Дальше работаем с укороченной системой, т. к входит только в 1-е уравнение.

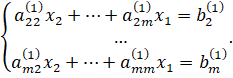
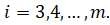
2-й шаг. На этом шаге исключаем неизвестное из уравнений с номерами Если ведущий элемент второго шага, то из укороченной системы аналогично исключаем неизвестное и получаем матрицу коэффициентов такого вида:

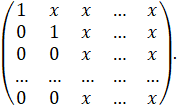
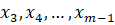
Аналогично указываем действия для неизвестных и приходим к системе:

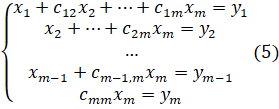
Эта система с верхней треугольной матрицей:

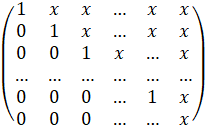
Обратный ход метода:

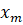
Из последнего уравнения системы (5) находим, из предпоследнего, …, из первого уравнения — .

Общая формула для вычислений:

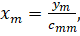
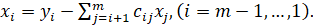
Для реализации метода Гаусса требуется примерно арифметических операций, причем большинство из них приходится на прямой ход.

Ограничение метода единственного деления заключается в том, что ведущие элементы на k-ом шаге исключения не равны нулю, то есть.

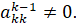
Результат работы программы (метод Гаусса):

Метод наискорейшего спуска:

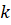
Так как мы используем итерационный (приближенный) метод, значения неизвестных вычисляем приближенно (три, четыре знака после десятичной точки), то, подставляя значения неизвестных в исходную систему, справа получим не ноль, а некоторые значения, называемые невязкой первого, второго, … уравнений наом шаге.

Представим систему линейных уравнений в следующем виде:

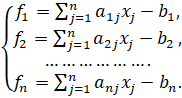
(4.1).

Запишем выражение (4.1) в операторной форме:

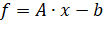
. (4.2).

Здесь приняты следующие обозначения:

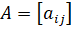
;;. (4.3).

В методе скорейшего спуска решение ищут в виде.

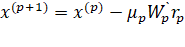
(4.4).

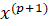
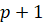
где и — векторы неизвестных на и шагах итераций; вектор невязок наом шаге определяется выражением:

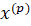
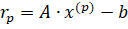
(4.5).

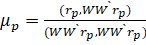
(4.6).

В формуле (4.6) используется скалярное произведение двух векторов, которое определяется следующей формулой:

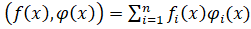
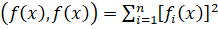
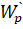
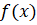
В формуле (4.6) _ транспонированная матрица Якоби, вычисленная на k-ом шаге. Матрица Якоби вектор — функции определяется как.

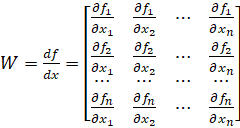
Нетрудно убедиться, что для системы (2) матрица Якоби равна.

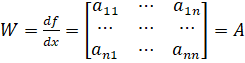
В качестве нулевого приближения можно взять.

.

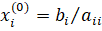
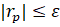
В методе градиента итерационный процесс естественно закончить при достижении, вектор невязок входит в вычислительную формулу.

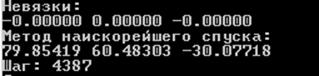
Результат работы программы (метод наискорейшего спуска):

Блок-схема Код программы:

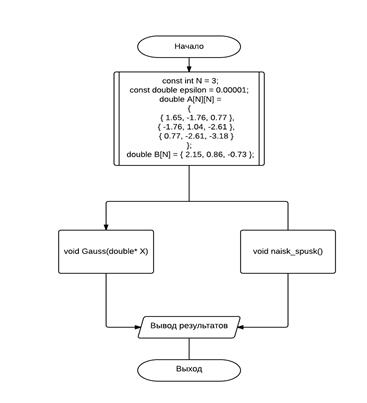
#include.

#include.

using namespace std;

const int N = 3;

const double epsilon = 0.1;

double A[N][N] =.

{.

{ 1.65, -1.76, 0.77 },.

{ -1.76, 1.04, -2.61 },.

{ 0.77, -2.61, -3.18 }.

};

double B[N] = { 2.15, 0.86, -0.73 };

void Gauss (double* X).

{.

double Q[N — 1];

for (int k = 0; k < N — 1; k++).

{.

for (int i = 0; i < N — 1; i++).

Q[i] = A[i + 1][k] / A[k][k];

for (int i = 0, j = k; j < N — 1;).

{.

A[j + 1][i] = A[j + 1][i] - Q[j] * A[k][i];

if (i == N — 1).

{.

B[j + 1] = B[j + 1] - Q[j] * B[k];

j++;

i = 0;

}.

else i++;

}.

}.

X[N — 1] = B[N — 1] / A[N — 1][N — 1];

double s;

for (int i = N — 2;; i—).

{.

s = 0;

for (int j = i + 1; j < N; j++).

s += A[i][j] * X[j];

X[i] = (B[i] - s) / A[i][i];

if (!i).

break;

}.

cout << «Метод Гаусса.» << endl;

for (int i = 0; i < N; i++).

cout << fixed << X[i] << ' ';

cout << endl;

}.

void Nevyazki (double* X).

{.

double D[N];

cout << «Невязки: «<< endl;

double s;

for (int i = 0; i < N; i++).

{.

s = 0;

for (int j = 0; j < N; j++).

s += A[i][j] * X[j];

D[i] = B[i] - s;

}.

for (int i = 0; i < N; i++).

cout << D[i] << ' ';

cout << endl;

}.

void naisk_spusk ().

{.

double Xp[N], AXp[N], rp[N], TA[N][N], A_[N][N], AA_r[N], Mu[N], A_r[N];

double temp, temp1, temp2;

bool t[N] = { 0, 0, 0 };

int i, j, k, it, q = 0;

for (i = 0; i < N; i++).

Xp[i] = B[i] / A[i][i];

for (i = 0; i < N; i++).

for (j = 0; j < N; j++).

TA[i][j] = A[j][i];

for (it = 0;; it++).

{.

for (i = 0; i < N; i++).

{.

AXp[i] = 0;

for (j = 0; j < N; j++).

AXp[i] += A[i][j] * Xp[j];

rp[i] = AXp[i] - B[i];

}.

for (i = 0; i < N; i++).

{.

for (j = 0; j < N; j++).

{.

A_[i][j] = 0;

for (k = 0; k < N; k++).

A_[i][j] += A[i][k] * TA[k][j];

}.

}.

for (i = 0; i < N; i++).

{.

AA_r[i] = 0;

for (j = 0; j < N; j++).

AA_r[i] += A_[i][j] * rp[j];

}.

temp1 = temp2 = 0;

for (j = 0; j < N; j++).

{.

temp1 += rp[j] * AA_r[j];

temp2 += AA_r[j] * AA_r[j];

}.

temp = temp1 / temp2;

for (i = 0; i < N; i++).

Mu[i] = temp;

for (i = 0; i < N; i++).

{.

A_r[i] = 0;

for (j = 0; j < N; j++).

A_r[i] += TA[i][j] * rp[j];

}.

for (i = 0; i < N; i++).

Xp[i] = Xp[i] - Mu[i] * A_r[i];

q = 0;

for (i = 0; i < N; i++).

{.

if (fabs (Mu[i] * A_r[i]) < epsilon).

t[i] = true;

q += t[i];

}.

if (q == 3).

break;

}.

cout << «Метод наискорейшего спуска:» << endl;

for (i = 0; i < N; i++).

cout << fixed << Xp[i] << ' ';

cout << endl;

cout << «Шаг: «<< it << endl;

}.

int main ().

{ setlocale (LC_ALL, «RUS»);

double* X = new double[N];

cout.precision (5);

Gauss (X);

Nevyazki (X);

naisk_spusk ();

delete[] X;

return 0;}.

Выводы:

В точных методах решение x находится за конечное число действий, но из-за погрешности округления и их накопления прямые методы можно назвать точными, только отвлекаясь от погрешностей округления.

В итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге.