Вывод интегральных уравнений для полупространства

Для вывода интегральных уравнений для полупространства с выпуклой границей рассмотрим следующую матрицу:

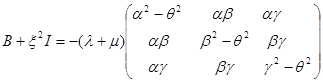
. (1.14).

Ее определитель D после вычислений принимает вид:

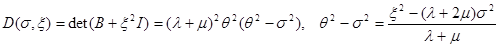
(1.15).

Вычисляем обратную к (1.14) матрицу:

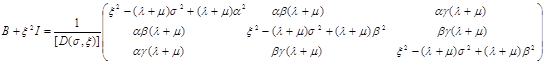
(1.16).

В дальнейшем элементы матрицы (1.16) будут обозначаться c_km.

Таким образом, имеем:

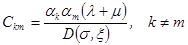
(1.17).

.

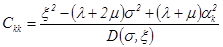
Теперь подействуем слева на соотношение (1.13) матрицей (1.16), после вычисления найдем:

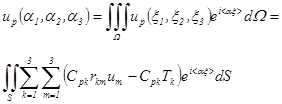
(1.18).

p=1,2,3. Для вывода интегральных уравнений, связывающих на границе перемещения u_m и напряжения T_k нужно изучить аналитические свойства функции .

Учитывая геометрию тела, заключаем, что она должна быть аналитически продолжаемой по параметру ₃ в верхнюю полуплоскость. Это вытекает из свойства области, описываемой неравенством .

Для выяснения условия, обеспечивающего аналитическую продолжимость решения, изучим распределение особенностей в представлении функции U_p. Все особенности этих функций описываются уравнением:

(1.19).

Находим корни этого уравнения:

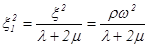
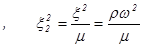
(1.20).

.

Таким образом, особенности функций описываются корневыми множествами функций трех комплексных переменных вида:

(1.21).

Эти корневые множества представляются аналитическими подмногообразиями в C³ комплексной размерности, равной двум. Разрешая уравнение относительно ₃, получаем представление корневых множеств вида:

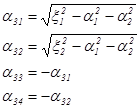
Здесь у радикала выбраны такие ветви, что.

при (1.22).

В этом случае при.

имеем.

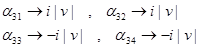
(1.23).

Поскольку область содержит положительную полуось, то функции U_p не должны иметь особенностей по параметру ₃ в верхней полуплоскости, т. е. должны быть аналитически продолжимыми в область . Следовательно, правая часть в выражении (1.18) должна быть ограниченной при и .

Для построения вытекающих из этого условия соотношений положим в (1.18):

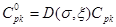
(1.24).

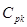
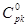
Тогда для ограниченности U_p достаточно потребовать обращения в нуль при и выражений (1.18), в которых вместо взято .

Выполнив эти подстановки, приходим к выражениям вида:

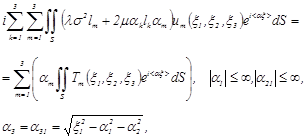
(1.25).

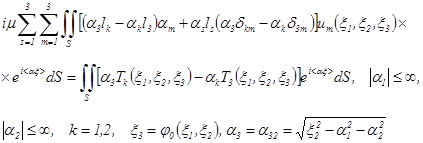
(1.26).

Здесь l_k — функция параметров. Соотношения (1.25), (1.26) являются своеобразной формой записи интегральных уравнений, связывающих заданные на границе S тела напряжения T_k и перемещения u_m.

Так, если рассматривается краевая задача теории упругости I рода, т. е. при заданных на границе S напряжениях, то правые части соотношений (1.25), (1.26) — известные выражения. И из уравнений необходимо найти перемещения u_m, стоящие в левых частях.

Если же рассматривается краевая задача теории упругости II рода, т. е. при заданных на границе S. перемещениях, то, наоборот, левые части соотношений (1.25), (1.26) известны, а определению подлежат стоящие в правых частях функции Т_k.

В случае смешанной задачи теории упругости, когда на одном множестве S¹ поверхности S заданы напряжения Т_k, а на другом S² -перемещения и_m, соотношения (1.25), (1.26) представляют собой систему интегральных уравнений, неизвестные которых расположены и в левой, и в правой частях в зависимости от того, по какому множеству осуществляется интегрирование. Важно, что на одном и том же множестве не могут быть одновременно либо только неизвестные и справа и слева, либо только известные функции. теория упругость месторождение полупространство Допустим, что удалось решить интегральные уравнения (1.25), (1.26) для перечисленных выше краевых задач теории упругости. Тогда известными функциями на всей поверхности S оказываются как перемещения и_m, так и напряжения T_k.. Внесем их в (1.18).

Геометрия задачи (полупространство) позволяет применить преобразование Фурье. Вообще преобразования Фурье при решении краевых задач теории упругости наиболее эффективно в тех случаях, когда упругое тело занимает объем, содержащий бесконечно удаленные точки, и все границы тела параллельны тем координатным осям, по которым берется преобразование. Свойства тела вдоль этих направлений также должны быть постоянными, но могут меняться в перпендикулярных направлениях. Преобразование Фурье не применимо по тем координатам, вдоль которых свойства среды непрерывно меняются.

В результате выражение для u_p(x₁, x₂, x₃) после применения формул обращения Фурье можно представить в виде:

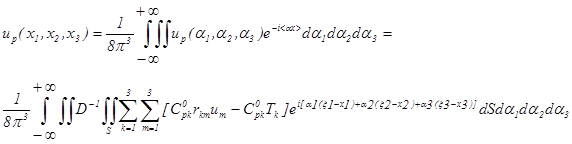
(1.27).

Интеграл по параметру ₃. вычисляется по теории вычетов.

Из соотношения (1.11), (1.12) видно, что решение содержит волны уходящие от поверхности S на бесконечность.

Полупространство с плоской границей

Рассмотрим частный случай исследуемой задачи, когда поверхность вырождается в плоскость, совпадающую с координатной плоскостью x₃=0. В этом случае внешняя нормаль к поверхности остается неизменной в любой точке и имеет компоненты.

(1.28).

Кроме того, надо принять ₃=0 на S, а также равенства:

(1.29).

Внесем значения указанных параметров в интегральные уравнения (1.11), (1.12). Тогда в подынтегральных выражениях члены.

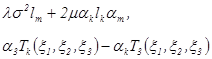
оказываются постоянными, не зависящими от параметров и их можно вынести за знак интегралов. Введем следующие обозначения:

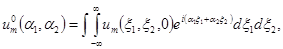
(1.30).

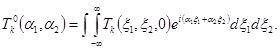
Интегральные уравнения (1.11), (1.12) можно переписать в виде:

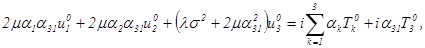
(1.31).

.

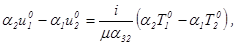
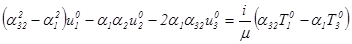
Эти соотношения полностью совпадают с уравнениями, получающимися при удовлетворении граничных условий в краевой задаче об установившихся колебаниях упругого полупространства. Если на границе задается вектор напряжений Т_о, то для получения перемещений на границе левые части соотношения (1.31) необходимо разрешить относительно компонент вектора U⁰.

В матричном виде систему (1.31) можно представить в форме.

(1.32).