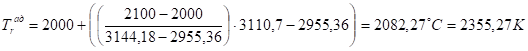Адиабатическая температура горения

Для определения адиабатической температуры горения необходимо знать объем продуктов горения и количество теплоты, выделившееся при сгорании вещества. Объем продуктов горения находят из уравнения материального баланса, а теплоту сгорания вещества по закону Гесса. Расчет адиабатической температуры горения проводят методом последовательных приближений, используя зависимость теплосодержания продуктов горения от температуры.

Уравнение материального баланса позволяет рассчитывать количество воздуха, необходимое для горения любого горючего вещества и количество образующихся продуктов горения.

Минимальное количество воздуха, необходимое для полного сгорания единицы количества (кг, кмоль, м³) горючего вещества, называется теоретическим количеством воздуха .

Запишем уравнение материального баланса горения Трет-амиловый спирт ().

В общем виде формула для расчета количества воздуха:

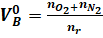
(1).

где, _, - число кмолей кислорода, азота и горючего вещества в уравнении материального баланса, кмоль.

А для расчета объема продуктов горения:

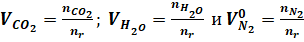
(2).

Где, , — количество кмолей вещества в правой части уравнения материального баланса, а — объем азота из воздуха, участвовавшего в горении, кмоль/кмоль.

Общий объем продуктов горения определяется по формуле:

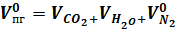
(3).

Подставив значения получаем:

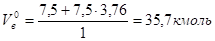
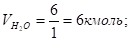
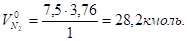
Общий объем продуктов горения:

При расчетах температуры горения пользуются величиной Q_n так как при температуре горения вода находится в газообразном состоянии. Значения низшей теплоты сгорания вещества (тепловой эффект химической реакции) приводится в справочной литературе.

Эта величина может быть рассчитана по закону Гесса, который говорит о том, что тепловой эффект химической реакции равен разности сумм теплоты образования продуктов реакции и теплоты образования исходных веществ:

(4).

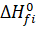
где — теплота образования i-того вещества,.

n_i — количество молей i-го вещества.

Теплота образования сложного вещества равна количеству теплоты, выделившейся при его образовании из простых веществ.

Теплота образования простого вещества, молекулы которого состоят из атомов одного элемента, например, N₂, O₂, H₂, S, C принимается равной нулю.

При сгорании Трет-амиловый спирт ().

низшая теплота сгорания, согласно закону Гесса, равна:

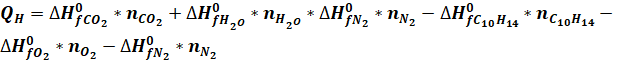
(5).

Учитывая, что кислород и азот, простые вещества, для них ?Н⁰_??=0.

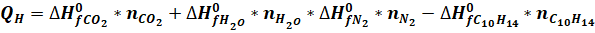
(6).

Подставляя значения теплоты образования CO₂, H₂O и С₁₀Н₁₄ из табл. II приложения, окончательно получим:

Под температурой горения понимают максимальную температуру, до которой нагреваются продукты горения. Принято адиабатическую температуру горения, рассчитываемую учета потерь тепла в действительную температуру теплопотери.

Температура горения зависит от концентрации горючего в горючей смеси. Если горение происходит с избытком воздуха, т. е. при б > 1, то выделившееся в результате сгорания тепло частично затрачивается на нагрев этого лишнего воздуха.

В горючей смеси с б < 1 из-за недостатка воздуха полное сгорание горючего вещества произойти не может, поэтому и тепловыделение в такой смеси будет неполным. Из этого можно сделать вывод, что максимальная температура горения будет при сгорании стехиометрической смеси, т. е. при б = 1.

Адиабатическую температуру горения вещества находим при условии отсутствия теплопотерь (з=0) для стехиометрической смеси горючего с воздухом, т. е. при б=1.

Так как теплопотери отсутствуют, то все выделившееся тепло идет на нагревание продуктов горения. Среднее теплосодержание продуктов горения будет составлять:

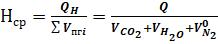
(7).

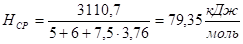
Воспользовавшись зависимостью теплосодержания газов от температуры (табл. IV приложения), можно установить, какой температуре соответствует такое теплосодержание. Лучше всего это сделать, ориентируясь на азот, так как его больше всего в продуктах горения. Из табл. IV приложения видно, что при температуре 2400 °C теплосодержание азота 81,5 кДж/моль. Уточним, сколько потребовалось бы тепла, чтобы нагреть продукты горения до такой температуры.

При Т₁ = 2400 °C.

Q₁ = H_CO2 • V_{CO 2} + H_Н2О • V_Н2О + H_N2 • V_N2, (8).

подставляя численные значения теплосодержаний этих газов из табл. IV приложения, получим:

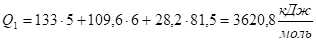
Но это больше, чем выделилось тепла в результате реакции горения.

Q₁ > Q_н

Поэтому можно сказать, что температура горения меньше, чем 2400⁰С.

Определим, сколько тепла потребуется для нагревания продуктов горения до 2300 °C.

При Т₂ = 2300 °C.

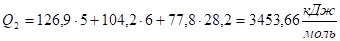
Q₂ > Q_н, значит Т_г < 2300 °C Сделаем следующий шаг (в этом и состоит суть метода последовательных приближений), выберем Т₃ = 2200 °C, при этой температуре:

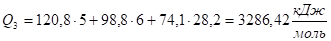
Q₃ > Q_н

Определим, сколько тепла потребуется для нагревания продуктов горения до 2100 °C.

При Т₄ = 2100 °C.

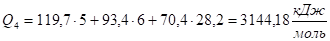
Q₄ > Q_н

При Т₅ = 2000 °C.

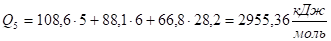
Q₅ уже меньше, чем Q_н, из этого можно сделать вывод, что температура горения имеет значение между 2000^°С и 2100^°С.

Уточним эту температуру линейной интерполяцией между двумя этими ближайшими значениями:

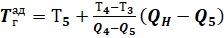
(9).