Системы координат. 
Курс общей физики

Значения физической величины удобно изображать точками на числовой оси, для построения которой необходимо на прямой выбрать положительное направление, начало отсчета и масштаб. Если в каких-либо задачах приходится иметь дело с двумя и более величинами, то совокупность значений этих величин изображают точкой на плоскости или в пространстве.

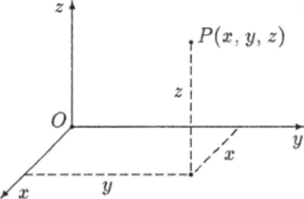
Рис. Ц. Координаты точки в пространстве.

Пусть в некоторой задаче независимыми являются три величины, которые обозначим х, у, г. Для того чтобы придать этим величинам геометрический смысл, построим три числовые оси, на которых будем откладывать значения х, у, z соответственно. Если эти оси взаимно перпендикулярны и проходят через одну точку, то говорят, что в пространстве задана декартова прямоугольная система координат, которая называется так в честь французского ученого Рене Декарта (1596 — 1650). Точку пересечения осей называют началом координат, а сами оси — координатными осями, каждой из которых приписывают порядковый номер. Первая ось называется осью абсцисс, или осью х, вторая — осью ординат, или осью у, а третья — осью аппликат, или осью z. Геометрический смысл, который можно придать совокупности {х, у, г] трех величин, заключается в том, что с их помощью можно отметить точку в пространстве.

Используя систему координат, произвольной точке Р пространства можно поставить в соответствие три числа х, у, z (рис. 1.4), которые называются ее координатами. Такое соответствие символически записывают как Р (х, у, г). Координата х точки Р (абсцисса) есть расстояние от этой точки до координатной плоскости yz (где х = 0), взятое с учетом знака. Аналогично определяются координаты у и г (ордината и аппликата).

Указанным способом в пространстве можно построить несколько декартовых прямоугольных систем координат, которые отличаются одна от другой положением начала координат и направлением координатных осей. Разумеется, координаты одной и той же точки пространства в различных системах координат отличаются друг от друга. Пусть х, у, г есть координаты точки Р относительно одной системы координат, а х, r/i, zj — координаты этой же точки относительно другой системы. Координаты xi, 2/i, z связаны с координатами х, у, z соотношениями.

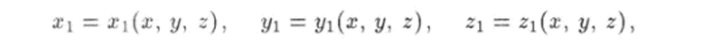
которые называются формулами преобразования координат.

Пусть в каждой точке Р пространства задано значение некоторой физической величины р: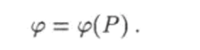

В таком случае говорят, что величина р есть функция точки в пространстве. Если выбрана прямоугольная декартова система координат, то можно записать равенство.

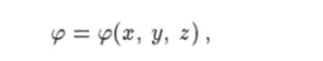
которое выражает зависимость величины р от координат точки пространства.

Величина р называется скалярной величиной, или скаляром, если ее значение в произвольной точке пространства не зависит от выбора системы координат. Примерами скалярных величин могут служить плотность, давление и температура вещества. Если каждой точке пространства поставлено в соответствие значение скалярной величины, то такое соответствие называется скалярным полем. Иначе говоря, скалярное поле есть скалярная функция точки пространства.