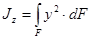Моменты инерции плоски фигур

Осевым, или экваториальным, моментом инерции площади фигуры называют интеграл произведений элементарных площадей на квадраты расстояний от рассматриваемой оси.

Полярным моментом инерции площади фигуры относительно данной точки (полюса) называют интеграл произведений элементарных площадей на квадраты их расстояний от полюса:

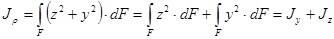
Если через полюс проведена система взаимно перпендикулярных осей и, то. Из выражения имеем.

Отметим, что величины осевых и полярных моментов инерции всегда положительны.

Центробежным моментом инерции называют интеграл произведений площадей элементарных площадок на их расстояния от координатных осей и :

В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным. Очевидно, что, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называют главными осями инерции.

Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут ее главными осями инерции Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями.

Моменты инерций сложных сечений.

В расчетной практике часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции относительно различных осей даны в сортаменте.

При вычислении нестандартных сложных сечений последние можно разбить на отдельные простые части, моменты которых известны. Из основного свойства интеграла суммы следует, что момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.

Если в сечении есть отверстие, его обычно удобно считать частью фигуры с отрицательной площадью.