Механические испытания горных пород

Основные теоретические положения

Модуль упругости (модуль Юнга — Е, Па), коэффициент Пуассона (н) и пределы прочности при одноосном сжатии у_сж и растяжения у_р являются важнейшими показателями механических свойств горных пород, необходимых при проектировании и ведении горных работ.

Пределы прочности при сжатии у_сж и растяжении у_р — это предельные значения одноосного напряжения при котором происходит разрушение породы. горный порода прочность массив Модуль упругости Е — коэффициент пропорциональности между действующими нормальными напряжениями и соответствующей им относительной продольной упругой деформации.

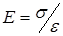
или (1.1).

Коэффициент Пуассона н — это отношение между относительными поперечными и относительными продольными деформациями ().

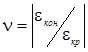
(1.2).

Модуль сдвига G — это коэффициент пропорциональности между касательными напряжениями ф и соответствующей упругой деформации сдвига. Модуль упругости Е и модуль сдвига G соответствует основным видам напряжений и деформаций. Они связаны с коэффициентом Пуассона следующей зависимостью:

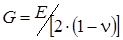
(1.3).

Первый раздел курсовой работы

Выбираем вариант задания

Вариант № 14.

Тип материалатуф Диаметр образцаD = 0,036 м.

Длина образцаL = 0,081 м.

Определим разрушающую силу

Проводим 6 испытаний образца породы на сжатие и растяжение. Доводим прикладываемую нагрузку до разрушения. По формулам 1.4 и 1.6 рассчитываем среднее значение разрушающей силы F, среднеквадратичное отклонение S и коэффициент вариации k_в.

кН (1.4).

гдеF — среднее значение разрушающей силы по n испытаниям, кН;

F_i — значение разрушающей силы в каждом опыте;

n — количество опытов.

Находим среднеквадратичное отклонение S и коэффициент вариации k_в, который характеризует точность лабораторных испытаний:

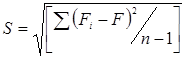
кН (1.5).

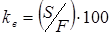
(1.6).

Результаты расчетов сводим в таблицу 1.

Таблица 1 — Результаты определения разрушающей силы.

Определяем нагрузку для упругих испытаний породы

Находим силу F_y, при которой деформации остаются упругими, т. е. не вызывающие разрушения образца и не дающие пластической деформации. По данным практики эта сила составляет 60−70% от разрушающей (здесь 60%).

Тогда сила, которую необходимо приложить к образцу:

• — при сжатииF_у сж.=131,6^.0,65=85,54 кН
• — при растяженииF_{у. раст.}=13,6^.0,65=8,84 кН

Определим поперечную и продольную абсолютные деформации образца при его упругом сжатии и растяжении

Для этого нагружаем образец до величины силы F_y и определим полученные деформации при сжатии и растяжении образца.

Опыт производим не менее 6 раз. Рассчитываем средние значения деформаций (d и dD), их среднеквадратичное отклонение (S, мм) и коэффициент вариации (k_в, %). Результаты расчетов сносим в таблицу 2.

Таблица 2 — Результаты определения абсолютных деформаций образца.

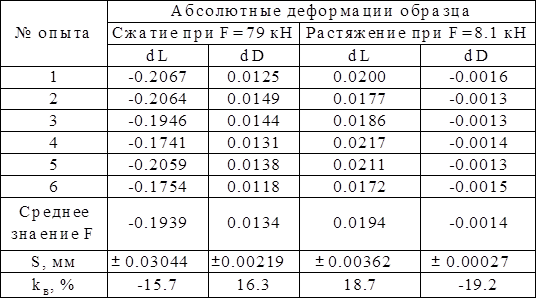
Определяем пределы прочности образца при сжатии и растяжении.

Для этого находим поперечную площадь, А по формуле:

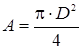
(1.7).

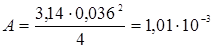
м².

Определим пределы прочности породы при сжатии и растяжении по формуле:

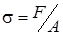
Па (1.8).

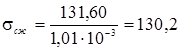
МПа.

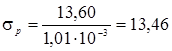
МПа Относительные деформации е_пр, е_поп определяем по формулам:

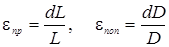
(1.9).

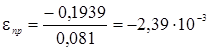
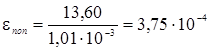
Определим коэффициент Пуассона по формуле 1.2.

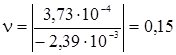
Определяем модуль упругости для материала образца по формулам 1.1.

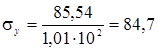
МПа.

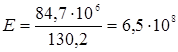
Рассчитываем модуль сдвига по формуле 1.3.

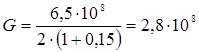
Строим линейный условный паспорт прочности.

Для этого используем теорию Мора и линейную аппроксимацию для огибающей кругов Мора. На диаграмме строим круги одноосного сжатия и растяжения, и проводим касательную к обеим кругам.

Геометрически определяем величину сцепления © и угол внутреннего трения (ц).