Требования. 
Разделение геологического разреза месторождения на пачки и выбор типа буровых долот

Основные требования для разделения геологического разреза на пачки (интервалы) одинаковой буримости, [2, с. 225]:

Непрерывность пачки (интервала).

При бурении пачки должны быть использованы однотипные буровые установки, буровые долота одного диаметра, турбобур одного типа и диаметра. Параметры режима бурения должны быть одинаковыми или близкими.

Горные породы, слагающие пачку, должны быть близкими по литологическому составу.

Проверка однородности пачки одинаковой буримости

Таблица 1. Проходка на долото.

Все члены вариационного ряда должны быть расположены в порядке увеличения.

(1).

где n — число членов ряда.

Для исключения грубых ошибок проводится проверка крайних значений вариационных рядов. Для значения Х₁ проверка делается следующим образом. Вычисляются левые части неравенств (2), (3), (4) и сравнивается со значениями К₁, К₂, К₃ из таблицы 2.

Таблица 2. Критерий К при надёжности оценки Р = 0,95.

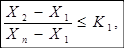
(2).

(3).

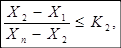
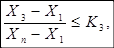
(4).

Если любое из неравенств не выполняется, то величина Х₁ призна? тся грубой ошибкой и должна быть из вариационного ряда исключена.

Аналогично делается проверка для значении Х_n.

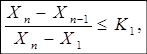
(5).

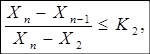
(6).

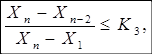
(7).

При невыполнении любого из неравенств величина Х_n из ряда исключается, а при невыполнении неравенства (7) исключается значение Х_n-1.

После исключения промахов определяются характеристики вариационных рядов: среднее значение Х и среднее квадратичное отклонение S.

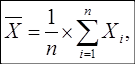
(8).

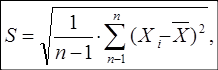
(9).

Для сравнения двух рядов (первого 1 и второго 2) вычисляется общее среднее квадратичное отклонение:

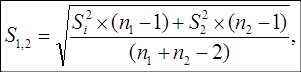
(10).

и параметр t_1,2 распределения Стьюдента разности — :

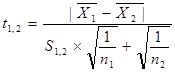
(11).

Значение t_1,2 сравнивается с табличным значением параметра распределения Стьюдента t (таблица 3) при заданной величине надёжности 0,95 и определённом числе степеней свободы m, который определяется по следующей формуле:

Таблица 3. Параметр распределения Стьюдента при P=0,95

В случае если t_1,2>t, то должен быть сделан вывод, что различие средних значений Х₁ и Х₂ статически значимо и пачки не должны быть объединены. Если t_1,2то различие значений Х₁ и Х₂ не значимо.

Таким образом, пачки должны быть признаны однородными, то есть, объединены в один интервал. Далее рассматривается вопрос о возможном объединении второй и третьей пачки, третьей и четвертой.

В конце раздела делается вывод о том, на какие пачки разделен разрез.

Проверочные расчёты однородности пачек одинаковой буримости:

Вариационный ряд 1 (400−1000 м.):

101<222<779<807<833<859<881<903<960<1036<1068<1080 (n₁=12),.

Проверка для значения Х₁:

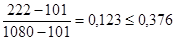
(К₁), условие неравенства выполняется.

(К₂), условие неравенства выполняется.

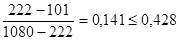
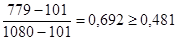
(К₃), условие неравенства не выполняется, то величина Х₁ исключается из вариационного ряда 1, и n=11.

Аналогичная проверка для значения Х_n:

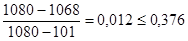
условие неравенства выполняется.

условие неравенства выполняется.

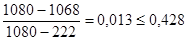
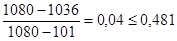
условие неравенства выполняется.

=857,09.

S₁=234,9.

Вариационный ряд 2 (1000−1500 м.):

66<150<163<176<189<200<211<240<277<293<299<1080 (n₂=12).

Проверка для значения Х₁:

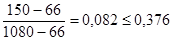
условие неравенства выполняется.

условие неравенства выполняется.

условие неравенства выполняется.

Аналогичная проверка для значения Х_n:

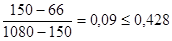
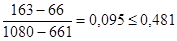
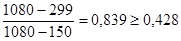
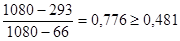
условие неравенств не выполняется, то величины Х_n и Х_n-1 исключаются из вариационного ряда 2, и n=10.

S₂=65,5.

Вариационный ряд 3 (1500−2000 м.):

50<66<69<76<100<111<140<177<189<193<199<980 (n₃=12).

Проверка для значения Х₁:

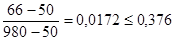
условие неравенства выполняется.

условие неравенства выполняется.

условие неравенства выполняется.

Аналогичная проверка для значения Х_n:

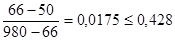
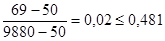
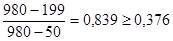
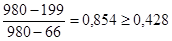
условие неравенств не выполняется, то величины Х_n и Х_n-1 исключаются из вариационного ряда 3, и n=10.

.

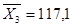
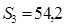
Проверяем возможность объединения интервалов в пачки одинаковой буримости.

Сравниваем вариационные ряды между собой путем вычисления общего квадратичного отклонения:

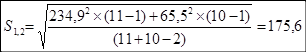
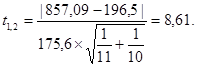
Степень свободы: m_1,2=11+10−2=19.

8,61>t=2,10 (таблица 3).

Если t_1,2>t, значит различие средних значений и значимо и пачки 1 и 2 не должны быть объединены.

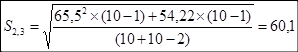
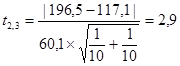
Степень свободы: m_2,3=10+10−2=18.

2,9>t=2,11 (таблица 3).

Если t_2,32>t, значит различие средних значений и значимо и пачки 2 и 3 не должны быть объединены.

Вывод:

Согласно произведенным расчётам по определению однородности пачек одинаковой буримости геологический разрез разделен на 3 пачки:

• 400−1000 м.
• 1000−1500 м.
• 1500−2000 м.