Характеристика понятия размерности

Понятие размерности

Понятие «числа измерений», или «размерности», не вызывает особых затруднений, пока речь идет о таких простых геометрических образах, как точки, линии, треугольники или многогранники. Отдельная точка или любое конечное множество точек имеет размерность нуль, отрезок — размерность 1, поверхность треугольника или сферы — размерность 2. Множество всех точек куба имеет размерность 3. Однако при желании обобщить понятие размерности на точечные множества более общих типов возникает необходимость в точном определении. Какую размерность следует, например, приписать множеству R, состоящему из всех точек оси х, у которых координаты х-рациональные числа? Множество рациональных точек на оси х всюду плотно, и потому, казалось бы, ему, как и самому отрезку прямой, надлежало бы приписать размерность 1. С другой стороны, между всякими двумя рациональными точками существуют иррациональные «дыры», как между всякими двумя точками конечного множества, и это говорит в пользу размерности 0.

Еще запутаннее обстоит дело с размерностью любопытного множества, впервые рассмотренного Кантором, построенного следующим образом. Из единичного отрезка 0? x?1 удалим среднюю треть (интервал), т. е. все точки х, удовлетворяющие неравенству Оставшееся точечное множество обозначим через С1. Множество C1 состоит из двух отрезков; удалим теперь из каждого отрезка его среднюю треть и то множество, которое останется, обозначим через С2. Повторим опять эту процедуру, удаляя среднюю треть у всех четырех отрезков; получим С3. Дальше таким же образом получим С4, С5, С6, …. Обозначим через С множество точек, которое останется, когда все средние трети будут удалены, т. е. С есть, другими словами, множество точек, принадлежащих одновременно всем множествам С1, С2, С3, …. В первой операции был удален интервал длины 1/3; во второй операции — два интервала, каждый длины 1/9, и т. д.; сумма длин всех удаленных интервалов равна.

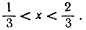
Бесконечный ряд в больших скобках есть геометрическая прогрессия, сумма которой равна итак, сумма длин удаленных интервалов составляет все-таки далеко не все точки отрезка удалены: множество С не пустое. Например, все точки, являющиеся концами удаленных отрезков.

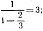
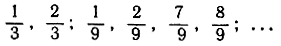
ему принадлежат. Можно легко убедиться, что множество С состоит в точности из всех тех чисел х, разложения которых в бесконечную дробь по основанию 3 могут быть написаны в форме.

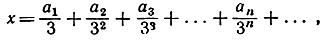
где всякое аn есть или 0 или 2, тогда как в аналогичном разложении для всякой удаленной точки среди чисел сn хоть раз встретится 1.

Какова же размерность множества С? Диагональный процесс, с помощью которого была доказана несчетность множества всех действительных чисел, может быть видоизменен таким образом, чтобы тот же результат получился и для множества С. Отсюда было бы естественно заключить, что множеству С надлежит приписать размерность 1. С другой стороны, С не содержит никакого, даже самого малого, отрезка, как и любое конечное множество; это сближает С с множествами размерности 0. Таким же образом, восставив в плоскости х, y из каждой рациональной точки или из каждой точки канторова множества перпендикуляр единичной длины к оси х (направляя его в сторону положительных значений у), мы получим множества, относительно которых может возникнуть сомнение — приписать ли им размерность 2 или 1.

Рис. Канторово множество

Впервые Пуанкаре (в 1912 г.) обратил внимание на необходимость более глубокого анализа и более точного определения размерности. Пуанкаре заметил, что прямая или кривая имеет размерность 1, так как любые две точки на ней можно разделить, удаляя одну-единственную точку (множество размерности 0); плоскость же имеет размерность 2 по той причине, что для разделения двух точек на плоскости нужно удалить целую замкнутую кривую (множество размерности 1). Это приводит к мысли о том, что понятие размерности имеет «индуктивную» природу: некоторому «пространству» следует приписать размерность n, если две точки в нем разделяются при удалении подмножества точек размерности n-1 (но удаления подмножества меньшей размерности уже не было бы достаточно). В сущности такого рода индуктивное определение неявно содержится уже в евклидовых «Началах», где одномерный образ толкуется как нечто, граница чего состоит из точек; двумерный образ — как нечто, граница чего состоит из линий; наконец, трехмерный образ — как нечто, граница чего состоит из поверхностей. размерность интервал теорема покрытие За последние годы была развита обширная теория — теория размерности. Определение размерности начинается с того, что разъясняется смысл термина «точечное множество размерности 0». Любое конечное точечное множество обладает тем свойством, что каждая его точка может быть заключена в сколь угодно малую область пространства, причем на границе области нет точек множества. Это свойство принимается теперь за определение размерности 0. Условимся ради удобства говорить, что пустое множество имеет размерность -1. В таком случае множество S имеет размерность 0, если оно не имеет размерности — 1 (т. е. если 5 содержит хоть одну точку) и если каждая точка S может быть заключена в произвольно малую область, граница которой пересекает S по множеству размерности — 1 (т. е. совсем не содержит ни одной точки S). Так, например, множество рациональных точек на прямой имеет размерность 0, так как каждая рациональная точка может быть рассматриваема как центр произвольно малого интервала с иррациональными концами. Канторово множество С также размерности 0, так как, подобно множеству рациональных точек, оно получается посредством удаления всюду плотного множества точек прямой.

Итак, мы уже определили понятия «размерность — 1» и «размерность 0». Теперь легко понять, что такое «размерность 1»: говорят, что множество S имеет «размерность!», если оно не есть ни размерности — 1, ни размерности 0 и если каждая точка S может быть заключена в произвольно малую область, граница которой пересекается с S по множеству размерности 0. Отрезок прямой обладает этим свойством, так как границей каждого промежутка является пара точек, т. е. множество размерности 0 по предыдущему определению. Дальше, продолжая таким же образом, мы можем последовательно определить, что такое размерность 2, размерность 3 и т. д., причем каждое следующее определение основывается на предыдущем.

Таким образом, говорят, что множество S имеет размерность n, если оно не имеет меньшей размерности и если каждая точка S может быть заключена в произвольно малую область, граница которой пересекается с S по множеству размерности n-1. Например, плоскость имеет размерность 2, так как любая точка плоскости может быть заключена в кружок произвольно малого радиуса, граница которого имеет размерность 1*. В обыкновенном пространстве никакое множество точек не может иметь размерность, большую чем 3, так как любая точка пространства есть центр произвольно малой сферы, граница которой имеет размерность 2. Но в современной математике термин «пространство» употребляется в более общем смысле; он обозначает любую систему объектов, для которой введено понятие «расстояния» или «окрестности», и такого рода абстрактные «пространства» могут иметь размерность, большую, чем 3. Простым примером является декартово n-мерное пространство, «точки» которого суть системы из п действительных чисел, взятых в определенном порядке:

P = (x1, x2, …, xn),.

Q = (y1, y2, …, yn),.

а «расстояние» между Р и Q определяется по формуле.

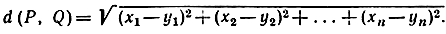
* (Сказанное не означает, что доказательство того, что плоскость имеет размерность, 2 в смысле нашего определения, уже закончено: остается доказать, что граница круга (окружность) имеет размерность 1 и что сама плоскость не имеет размерности 0 или 1. Эти утверждения можно доказать, как и аналогичные утверждения для высших размерностей. Все предыдущие рассуждения показывают, что приведенное выше общее определение размерности не стоит в противоречии с обычным его пониманием.).

Можно показать, что это пространство имеет размерность n. Пространство, которое не имеет размерности n, как бы велико ни было n, называется пространством бесконечной размерности. Известно много примеров таких пространств.

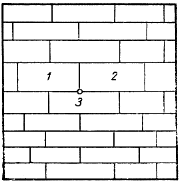
Рис. Теорема о покрытии

В теории размерности устанавливается одно чрезвычайно интересное свойство двумерных, трехмерных и вообще n-мерных фигур. Начнем с двумерного случая. Если какая-то простая двумерная фигура подразделена на достаточно маленькие «ячейки» (причем предполагается, что каждая ячейка содержит свою границу), то непременно найдутся такие точки, которые принадлежат сразу по меньшей мере трем ячейкам, какова бы ни была форма выбранных ячеек. Вместе с тем существуют такие разбиения фигуры на ячейки, что никакая точка фигуры не принадлежит сразу больше чем трем ячейкам. Так, если рассматриваемая двумерная фигура есть квадрат (рис. 131), то непременно имеются точки вроде той, которая сразу принадлежит трем ячейкам 1, 2 и 3, но для указанного на чертеже разбиения не существует точки, которая сразу принадлежала бы большему числу ячеек. Точно так же в трехмерном случае можно доказать, что если некоторая объемная фигура (тело) разбита на достаточно маленькие ячейки, то наверное существуют точки, принадлежащие по меньшей мере четырем ячейкам, и вместе с тем можно выбрать такие разбиения, что никакая точка не будет принадлежать сразу больше чем четырем ячейкам.

Все эти соображения приводят нас к следующей теореме, высказанной А. Лебегом и Брауэром: Если n-мерная фигура разбита на достаточно маленькие ячейки, то непременно существуют точки этой фигуры, принадлежащие сразу по меньшей мере n+1 ячейкам; вместе с тем возможно указать и такие разбиения, что ни одна точка фигуры не будет принадлежать сразу более чем т+1 ячейкам. Эта теорема характеризует размерность рассматриваемой фигуры: все фигуры, для которых теорема верна, являются n-мерными, все прочие имеют иную размерность. По этой причине указанная теорема может быть взята за определение размерности (так и делают некоторые авторы).

Размерность фигуры относится к числу топологических ее свойств: никакие две фигуры различных размерностей не могут быть топологически эквивалентными. В этом заключается замечательная теорема об «инвариантности размерности»: чтобы оценить ее должным образом, стоит напомнить другую теорему (доказанную на стр. 113), согласно которой множество точек квадрата имеет ту же мощность, что и множество точек отрезка. Соответствие между точками, установленное при доказательстве этой теоремы, не топологическое, так как требование непрерывности нарушается.